母と子の算数対話シリーズ

算数不安症（Math anxiety）という言葉をお聞きになったことがあ るでしょうか？ 日本語版ウィキペディアにはありませんが、英文版にはかなりの分量の情報があります。 その説明の前に、本小論のために多くの人にインタビューした質問の一部をご覧ください。

みなさんのお答えは、いかがでしょうか。 私たちは、高校一年生20人ほどに掛け算と足し算の質問を投げ掛けました。「えっ」という反応を示した生徒が70％を超えました。習ったはずですが、子どもたちは九々を暗記していますので、足し算の意識がないのかもしれません。中学生は数人に尋ねただけですが、質問のどれにも「習ってません」という答えでした。 3）と4）については、大人10数人に尋ねました。全員、このような表現は聞いたことがないといいます。言葉だけでなく、具体例を挙げて尋ねた結果です。

一方、5年生で学習する「割合」が、算数でつまずく単元と云われています。「平成27年度、29年度の学力テストでは基準量（もとにする量）や比較量（比べられる量）を求める問題の正答率はそれぞれ13.4％、13.5%という低さであった」と文科省の国立教育政策研究所が報告しています。 改善のために文科省は勿論、先生方も懸命な努力をなさっています。しかしながら、改善しているとは云い難い状況にあります。 私たちは、5年生でつまずく割合の原因が、2年生から習う分数にあるという結論に達しました。分数は比であり、割合のことですが、必ずしもそのような一貫性のある指導になっていないのが原因と思います。17年間小学校の先生をした後、現在教育委員会にお勤めの方も同様の指摘をなさっています。分数が、算数不安症の原因の一つなのは事実です。

算数不安症が人生に余計な負担を与える。AI時代の職業が数の能力と無縁ではありません。子どもたちの将来の可能性を狭めてしまってはならない。これが、本プロジェクトを始めた私たちの動機です。 ベイロック教授は、算数不安は、小学1年生からとおっしゃっています。 何時からかというのは、脳科学研究の大きな課題になっています。生後7か月の幼児が小さい数の足し算、引き算を認識しているという研究があります。マサチューセッツ工科大学AI研究所出身の先端企業研究開発役員を歴任した米国人エンジニアが、「個々の子どもは、生まれながらに独自の数のセンスを持っている。型に嵌めた計算手順主体の教育は、折角の個性を失わせる」と厳しい指摘をしています。 幼児教育で著名なカリフォルニアの教授がいます。4歳児が100までほとんどよどみなく数えるビデオを紹介して、数の認識はなくても言葉だけなら勘定できるとおっしゃっています。ThirteenやFourteenという言葉のパターンを覚えるわけです。ですから、ElevenとかTwelveというパターンにないものは教えられて記憶するわけです。ブロックを積み上げる幼児が、2個ずつ積み上げるのを見て、教わらなくとも偶数という感覚を持っていると報告している研究者もいます。同じことを日本の保育園の先生もおっしゃっていました。視覚から数のパターンを認識しているのです。 生後間もないうちに獲得する数のセンス（感覚）、言葉と数字のパターン認識、記憶などが相まって、算数の基礎を作り上げていくのです。就学前のお母さんとの有言無言の対話が如何に大切かというのがわかります。 本小論は、“数のセンス”を育むシリーズ（1）です。核心である分数に焦点を置きます。 心理学者や認知科学者の算数不安症の研究が契機になったと思われますが、2012年のPISAテスト結果を基にOECDが各国の算数不安状況を分析しています。

この報告書を読んでショックを受けました。日本の子たちが世界に類のない程の算数不安を抱えているのを知ったからです。文科省は勿論、内閣府も産業活性化のための教育に懸命の努力をしています。そのご努力には頭が下がります しかし、算数不安症を解消しなければ、折角のご努力の実が結ばないかもしれない。私たちはそう懸念します。まず、この図をご覧ください。

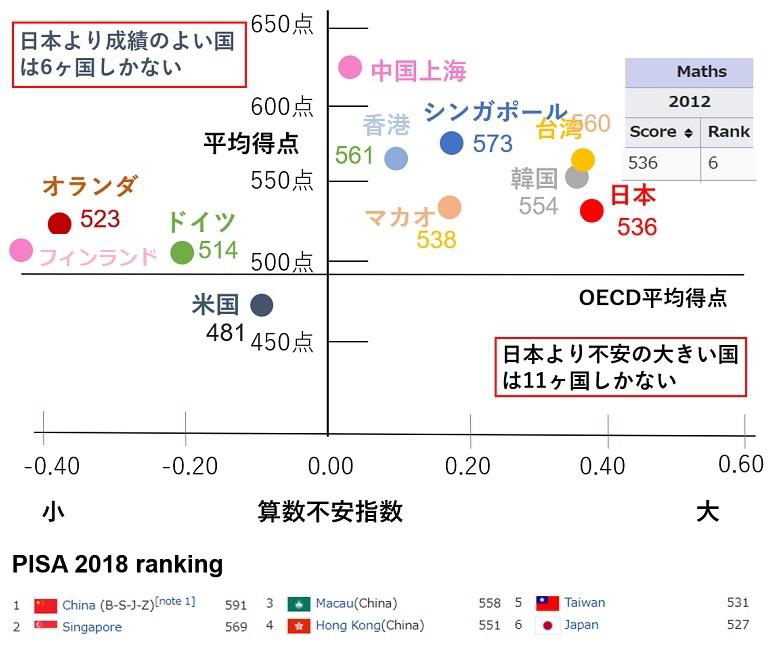
欧米諸国に比べるとアジアの子たちの算数不安は大きい傾向にあります。ベイロック博士の「態度や動機付けのアプローチを変える」という指摘が、自己認知度に表れています。

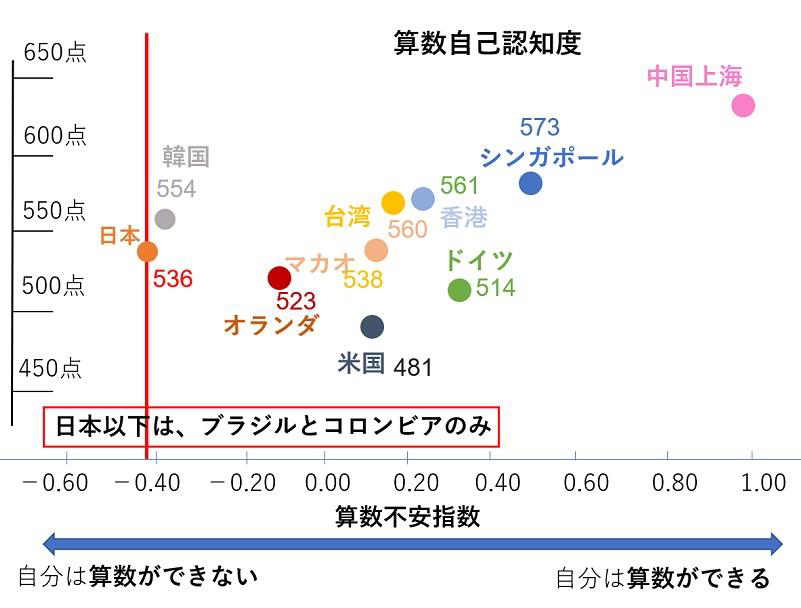
この自己認知度が問題です。成績は良いのにできないと思い込む。さらに、特異なのは、「努力してもできない」という自信喪失です。PISA得点が高い国で、このような傾向を示しているのは、日本と韓国だけです。 さらに、ベイロック博士の指摘「数学を回避する傾向」も明らかです。

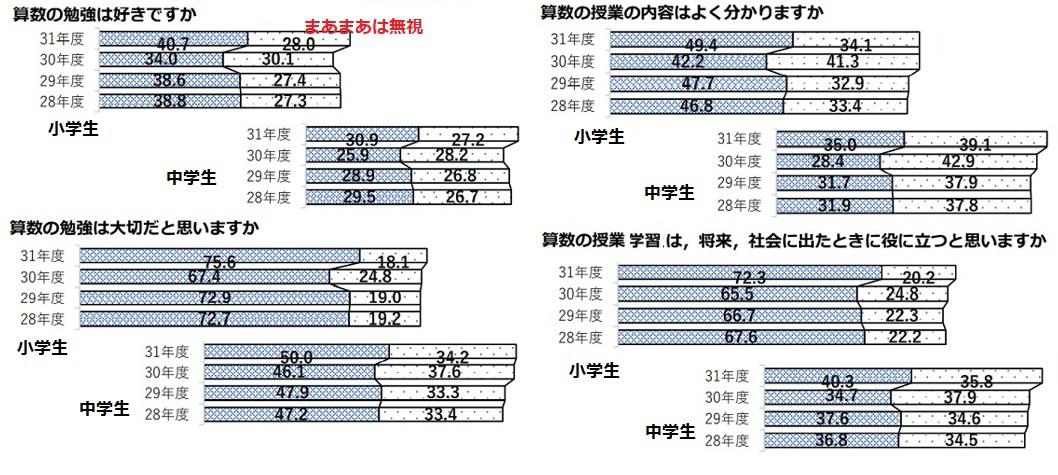
これも、国立教育政策研究所の調査結果です。小学生は、「算数は大切」、「社会に出たとき役に立つ」と思っています。しかし、中学生になるとどちらもガクンと減少します。「算数が好きか」と「授業の内容理解度」は相互作用要素です。内容がわかれば好きになる。わからなければ嫌いになる。それが普通です。 どきっとする本があります。桜美林大学リベラルアーツ学群数学者芳沢教授の本です。

まえがきに、「元にする量を1としたとき」という文章があります。これが、割合と分数を指導する一貫性のカギになります。 分数の指導には、先生方も大変なご苦労をされています。そのご苦労を知ることも父兄にとっては大切と思いますので、二つの例を紹介します。 最初は、公立小学校第５学年12名を対象にした「分数の除法の意味を実感的に理解するための教材の工夫」という山崎尚子先生の論文からです。

下線を引いた単位分数というのは、分子が1になる分数のことです。 3/4÷5が、3/4×1/5になって3/20になる論理をわかりやすく説明した指導研究です。山崎先生は、これまでも，計算の仕方を考えることが重視されてきたが，令和２年度より施行される新学習指導要領（平成29年告示）が、「目的に合った表現方法を用いて数の性質や計算の仕方などを考察する力となったので、より一層の工夫が必要」とお考えになったとおっしゃっています。 さらに、「実感的な理解」を得るためには，実際に操作して，その数量を目で見て確かめられる素材が有効であるが、（分数)÷(整数）の除法において，教科書（『みんなと学ぶ５年』p171，173）では，学習素材にじょうろ１杯分で水を撒ける花壇の面積とみかん１個分で作れるジュースの量を扱っている。これでは，どちらも実際に操作して，その数量を目で見て確かめるのは困難だと考える。それは，花壇では，児童が均質的に水を撒くのは大変困難であり，水を撒いた花壇の面積を数量として捉えるのは難しいからである。また，ジュースでは，液体量が流動的に変容するため，実際に操作を行った際に誤差が出やすく扱いにくいと判断した。そこで，本研究では，正方形のカステラ（具体物，半具体物）を素材とし，学習を進めることにした。この時，（分数)÷(整数）の計算の意味を実感的に理解するためには，単位分数の大きさの変化を視覚的に捉えられる図（以下「パラパラカステラ」と呼ぶ）が有効ではないかと予想した。そこで，図１に示す５枚のカードを重ねて示し，単位分数の変化を児童に提示することにした。これにより，具体物（本物のカステラ）や半具体物（カステラの図）を操作することで，単位分数の大きさの変化や（分数)÷(整数）の数量感覚について，実感的な理解が得られたかを分析することにしたそうです。 単位分数という言葉が何度も出てきます。ウィキペディアの項目“分数”に以下の記述があります。算数を言葉で表現するのが如何に難しくてわかりにくいか、我慢してください。

読んでいて嫌になりませんか？ 先生にならなくてよかったと思います、正直なところ。このややこしい話をわかりやすくかみ砕いて子どもたちに教えようとする先生は大変です。教えられる子たちも大変です。大人になりましたから我慢して何度か読むと、（今では）当たり前のことを云っているにすぎないと思いますが、言葉尻「現在では、分数n/mと単位分数1/mはどちらも同じ算術の規則に従い、どちらかを特別視することはない」というのを取り上げます。 数学をおやりの方の中には、エジプト分数に拘る方もいらっしゃるのではないか。若しかすると、そのために分数の指導に混乱があるのかもしれないという疑いからです。

さらに、こう続きます。

分母の17ですが、円をどのようにすれば、17分割できるのかわかりませんが、13/17の単位分子の足し算を円で図に示すとこのようになります。

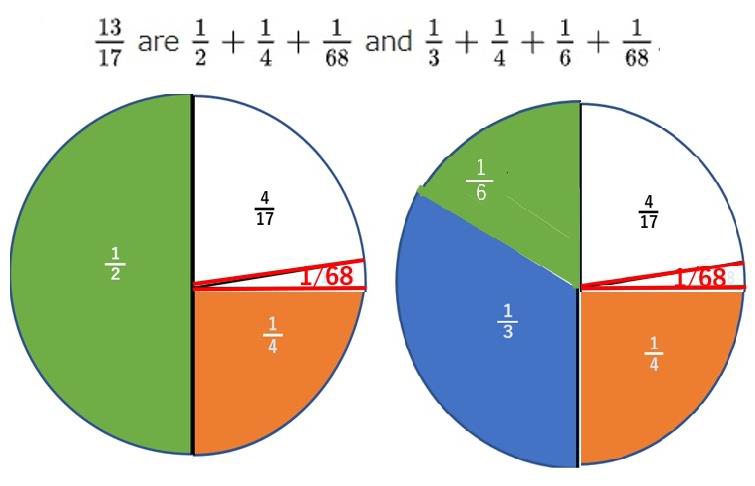
円が1単位です。1単位という言葉に注意してください。1単位を17等分割して13/17にする単位分数の足し算が二通りあると云っているのです。1単位に足りない分が4/17です。左の三つの単位分数の足し算、1/2＋1/4＋1/68は(34＋17＋１)/68=52/68=13/17になります。右の四つの単位分子の足し算は、1/3＋1/6＝1/2ですから左と同じくなります。 68分割をどうやるのか、私にはわかりません。360度は68で割り切れません。34でも割り切れません。17でも割り切れません。ですから、円が1単位ならどうやって分割するのか、私にはわかりませんので、1/68は目分量です。 しかし、 1単位が17キログラムの鉄の板なら17分割できます。 一分割1キログラムです。 1単位が34個のミカンなら17分割できます。 一分割2個です。 1単位が136個のおはじきなら17分割できます。 一分割8個です。 1単位が6800メートルなら17分割できます。 一分割400メートルです。 1単位が85分なら17分割できます。 一分割5分です。 1単位が7クラス合計生徒238人なら、17グループに分割できます。 一分割（グループ）14人です。 上から順に、重量、数量、距離、時間、人数です。それぞれの数は違います。 単位分数という言葉はどこにもありませんが、1単位という言葉を使いました。 芳沢教授の「元の量を1としたとき」というのが、1単位のことです。 1単位と単位分数の関係を明確にしておきます。 おはじきは、136個（1単位）を17分割して、一分割8個でした。 分数にすると、8/136=1/17（単位分数）です。 時間は、85分（1単位）を17分割して、一分割5分でした。 分数にすると、5/85=1/17（単位分数）です。 次の図をお子さんにきちんと教えたらよいと思います。算数不安症の原因、分数制覇です。

3/4という分数の意味を正しく教えてください。学校でもケーキを4分割して指導はしています。しかし、1単位という単位概念の指導が十分とは思いません。実際、単位概念というのが難しいのは事実です。 分数は、1単位を何等分（分割）したかが分母になり、分割したもの（単位分数）がいくつあるかを示すのが分子です。この文章を書いていて、正直なところ単位分数という言葉が邪魔です。ややこしくなります。 分母と分子を逆にしたものを逆数と云いますが、4/3を掛ける意味は、3/4を3等分、つまり1単位から見れば1/4を4個足すということです。 掛け算は足し算と習いましたかという最初のアンケート調査の意図は、分数でも同じというのを理解しているだろうか知るためでした。 分数の掛け算は分母同士、分子同士を掛けますから12/12=1になりますが、その論理はこの図に示す如く1単位に戻すということです。 「分数の掛け算は、分母同士、分子同士を掛ければいい」と習います。しかし、どうしてそうすればいいのかという理由を尋ねると、答えは戻ってきません。成績の良さそうな中1の子が、「そういう原理だからじゃないですか？」と反撃してきました。「その原理を尋ねているんだよ、きみ」とは云えませんでした。「ありがとう」とだけ。気が弱いものですから。したがって、単位分数からアプローチしたバラバラカステラ問題も、次のような単位概念からのアプローチで教えることもできます。3/4を直接5で割ります。

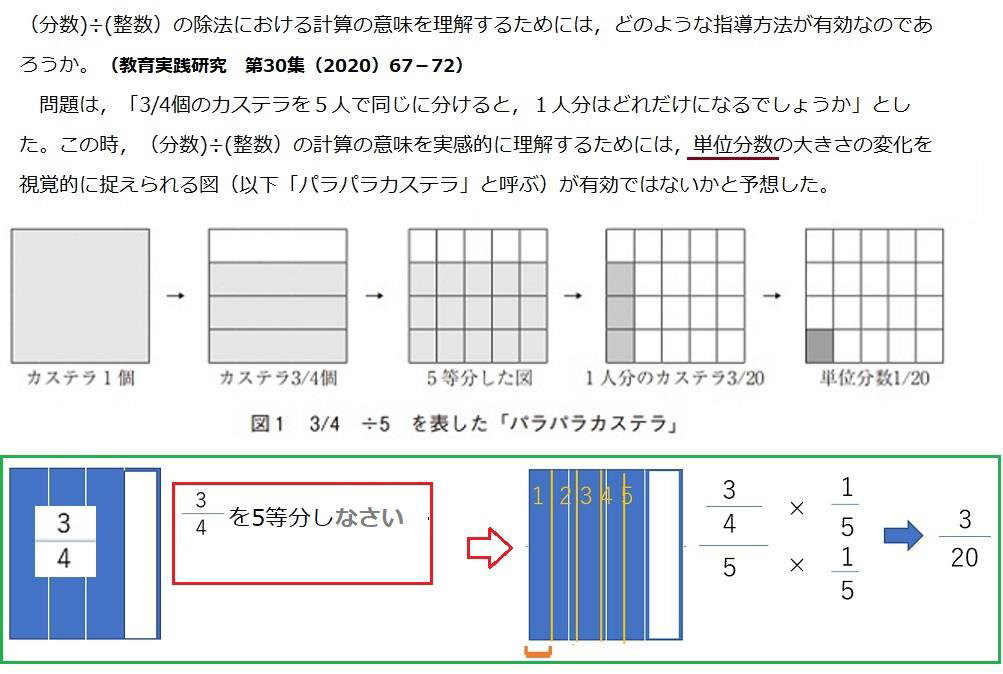
5で割る分数にして、分母を1にする。1単位にするわけです。 山崎先生の実感指導方法と併せて単位概念も指導していただければ、生徒の理解も深まるように思いますが、いかがでしょう。分数は整数の立体構造なので脳内イメージングに便利です。花壇の水やり分量もイメージングで解決します。今度は、分数同士の掛け算です。

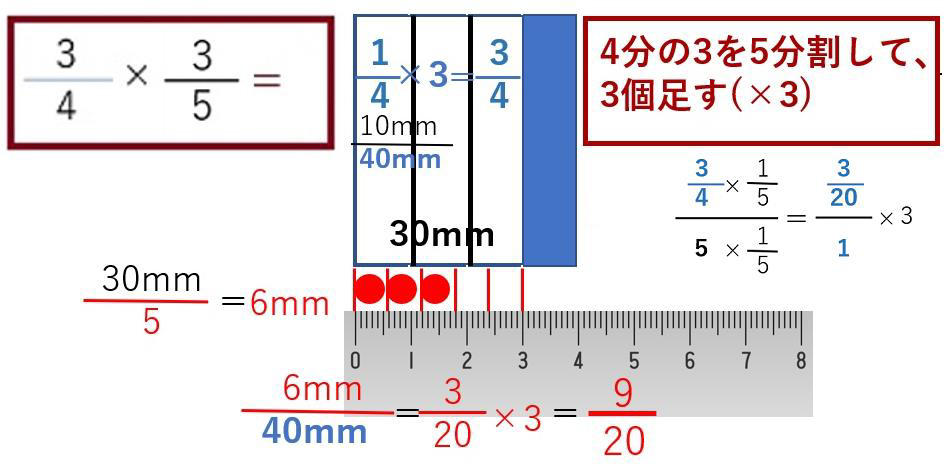
1単位を4分割したものを3個足した（×3）が白い部分で3/4です。わかりやすいように物差しに登場して貰いました。1単位の横の長さが40mmですから、3/4は30mmです。掛ける3/5の分母の5は、3/4を5分割するという意味ですから、30mmを分割すれば、一分割6mmになります。6mmは、1単位40mmの3/20です。赤丸一つに相当します。それを三つ足すので9/20になるわけです。学校で教えられた分母同士、分子同士を掛けろと同じ結果になります。これが分数の掛け算の論理です。 お話を伺った教育委員会の元先生も、この図を使って説明したとおっしゃっていました。私たちが推奨するのは、計算過程です。分母を1にする単位概念という考え方です。

1単位を20分割した9個という概念をしっかり指導していただけたらという願いです。5年生でつまずく割合を解決するには、どうしても分母を1にする単位概念を理解する必要があるからです。 加えて、「割合は比。分数の分母と分子は比」というのを何時、どのように指導するかという問題があります。2年生で分数を習い始めたときに、いきなり比と割合の関係を指導してくださいと先生方にお願いするのは難しいかもしれません。児童個々の理解度の差もありますから混乱を招く可能性もあります。しかし、ゆっくり家庭対話ならできると思いますというより、そうしなければならないと思います。その理由を述べます。 英国では成人の算数不安症が話題になっています。末尾に算数恐怖症を調べているオックスフォード大学とケンブリッジ大学のサイトURLを挙げましたが、オックスフォード大のサイトは算数不安症の原因に触れています。三つの原因があるといいます。 1） 短時間に答えを出さなければならないテスト時間のプレッシャー 2） 算数ができないと恥ずかしいというプレッシャー 3） 数学に自信のない先生の不安を生徒が感じる場合。 テスト時間制限が不安になるのは必然です。そこをどうすればいいかの答えはわかりません。しかし、算数ができないと恥ずかしいというプレッシャーは解決できます。 英国の子たちもそう思うというのは意外でしたが、日本には昔から「算数のできる子は頭の良い子」という妄信みたいなものがあります。今もそうです。高1の男の子が語ってくれました。「クラスで一目置かれるのは数学のできる子です。公式がすらすら出てくるので論理的と思われています」と。 どこと聞かれても云いませんが、ある駅で、高1の男の子三人、女の子二人のグループに、「君ら2進数習った？」と尋ねました。「2進数？」とスマホを開けて、「ああ、これか。憶えていない。私たちレベル低いんです」とあっけらか～んとした答えでした。元教師などの教育評論家やコンサルタントのサイトを数多く見ました。「お母さんは、算数がわからないと云ってはならない。子どもが安心して勉強しなくなる」と書いています。 “あっけらか～ん”ちゃんには無理かもしれませんが、逆じゃないかと思います。 「お母さんも苦手だったから一緒に勉強しようかな」と云った方が良いと思いますが、どうなのでしょう。 私たちのインタビュー調査では、「私も算数不安症でした」と答えてくれたお母さんは圧倒的です。10数人に尋ねた中で、ただ一人、72才になる女性で福祉関係カフェの副代表をされている方だけが、「私は算数が好きでした。答えがある科目なので好きでした。成績も良かったです」と答えてくれました。非常に稀な存在と思いました。お母さんの70%が、お子さんの算数が心配という調査はあります。私たちの調査母数は少ないですが、算数が苦手だったお母さんは結構多いという感触を持ちました。 「お母さんも苦手だったから一緒に勉強しようかな」の方が、子どもの「恥ずかしい」というプレッシャーを少しは解消するかもしれません。子ども同士のプライド問題の解消は容易ではないと思いますが、お母さんを上回ろうとやる気になる可能性も大きいと思います。さらに、数学が得意という人は変わり者ぐらいに思った方がいいと思います。変わり者というと叱られそうですが、頭の構造が違うのは確かです。私たちの仲間の一人は、60才のときハッキング技術をマスターしたいと思ったそうです。C言語を勉強しようと本屋に行って見繕っていたら、隣に小学高学年か中学生がいたので「きみ、Cわかるの？」と尋ねたら、「はい」というので、脳の構造が違うんだと思ってあきらめたと語っていました。人それぞれ構造が異なります。できるだけ早くに構造の違いに気づいて、特異な分野を見出す教育の方が大切と思います。頭の良し悪しとは必ずしも関係するわけではありません。

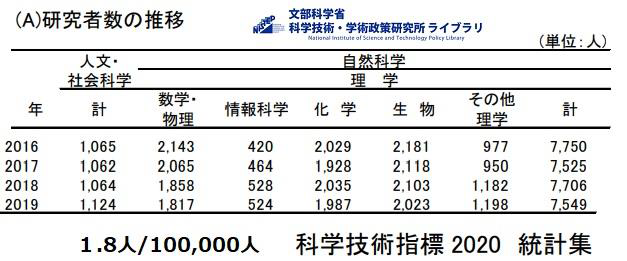
数学・物理研究者の数です。それぞれ専門分野で活躍する人は、そういう星の下に生まれたぐらいに思えばいいと思います。数学者の教育提言などを読むと、子どもたち全員を数学者にしたいのかと思うことすらあります。 内閣府が目標としているイノベーションは、研究者だけでできるものはありません。最も難しくて大変なのはマーケティングです。文科系の人の分野です。技術は定性的に理解して、技術を得意にする人を使いこなせばいいのです。 先生の不安の影響が50％という米国の研究調査はあります。 「先生になる資格試験では数学は51点取れればいい。数学の科目は多いので得意な分野と苦手な分野がある。苦手分野に関係する指導になると先生自体が不安になるので生徒に伝わって生徒まで不安になる」といいます。オックスフォード大学の調査には、「自信を持ったダイナミックな先生に教えられた生徒の算数不安は小さい」とあります。 人に何かを教えるというのは難しいです。誰にでも得手不得手はあります。不安に陥るのは当然です。しかも、先生方の仕事は重労働です。何でも先生の所為にすることなどできません。ですから、現実問題として家庭での対話を通してお子さんの算数不安を少しでも解消する以外に方法はありません。 原因が分数にあるというのがわかりましたから、そこを解決してやればいいだけのことです。小学生、中学生のときは算数不安症だったとしても、大人になる過程でいろいろなことを学び、知恵も豊富です。足し算はできますから、そこにちょっとだけ知恵を使えば、「割合は比。分数の分母と分子は比」というのもお子さんと対話できます。ただ、教えるのは大変ですので、どうしても、数の論理を理解しなくてはなりません。論理と云うと大げさに響きますが、どうってことはありません。数字のパターンですので、気付くか気付かないかだけです。気楽にお考え下さい。 そのために、若干詳しく説明したいと思います。日本語版ウィキペディアの分数の説明を引用します。が、その前に、ちょっと頭を休めましょう。

都美術館で開催された「水彩人23回展」に出品された光と水の画家平澤薫氏の作品です。氏も、子どもたち将来に幸あれと私たちのプロジェクトを応援してくださっています。ご許可をいただいたので掲載させていただきました。スマホ写真なので残念ですが、実物は印象派まったく異なる素晴らしい作品です。 こういう描き方のテクニックがあるのかと驚いた作品がありますので、順序をご覧ください。

完成一歩前の絵です。モデル農家の写真が以下ですが、画家の目を通すと何とも云い難い趣が出てくるものです。郷愁でしょうか。

鮮やかな色が再現できないので本当に残念です。 平澤氏は、工学部ご出身の都市設計関係のお仕事をされていた方で、水彩画を始めて15年とおっしゃっています。 氏の作品に出会ったのは数年前ですが、他の画家にはない独特の水の表現に感動しました。水が動く、生きているとでもいう感動でした。 スペインの風景画にそれがあります。

絵を描ける人も音楽をおやりの方もうらやましく思います。自分も描けたらな～、演奏できたらな～と思いますが、やはり脳の構造が違うのです。画家でも音楽家でも同じ人の作品を追求していると脳の構造が変化していることに気付きます。次にどんな変化が起きるのか、どのように作品に表れるのか。それが楽しみでもあります。 少しは頭休めになったでしょうか。 単位概念の話に戻ります。ウィキペディアの抜き書きスクリーンショットです。

この記述は極めて重要です。 最初の二行が、これまで述べた1単位の話です。 つまり、nという数字とmという数字に比の関係があれば、分数で表すとこうなると云っているのです。

(n/m)/1=n/mです。しつっこく云ってきた、1単位を分割した数が分母で、分割した数を足したものが分子ということです。nとmが比の関係にあればというのは、割合そのものです。ウィキペディアの比の項目を引用します。 比（ratio）とは2つ（または3つ以上）の数の関係を表したもの。数a,bについて、その比はa:bで表され、「a対b」とよむ。aを前項、bを後項（こうこう）という。また、前項と後項を入れ替えたb:aを元の比の逆比または反比という。 例えば、テレビ受像機には様々な大きさがあるが、横の長さを4等分したものと縦の長さを3等分したもの,あるいは,横の長さを16等分したものと縦の長さを9等分したものとが等しくなるのは,どの大きさのテレビでも変わらない。これをまとめて,それぞれ4:3,16:9で表す。 比において、前項と後項に（0以外の）同じ数をかけたものも同じ比である。つまり、a:b=ka:kb(k≠0)。 a:bにおいて、（b≠0のとき）a/bのことを比の値という。同じ比のものは同じ比の値をもつ。例えば、8:6の比の値8/6は約分すると4/3となり、4:3の比の値4/3と等しい。比の値a/bをそのまま比ということもある。またa/bは「bに対するaの比」とも言える。比の値は、bを単位量としたaの大きさを表すので、割合と同じ意味をもつ。また、a:b=a/b:1なので比の値は後項を1としたときの前項と言い換えることができる。後項を100とした前項(=100a/b)を百分率、またはパーセントという。 分数a/bは比であり、分母(b)を単位量とした分子(a)の大きさが割合と云っているのです。正答率57%の学力テスト問題で説明する方がいいと思います。

分数ではなく割り算の問題になっていますが、基準量（基準に対する大きさ）という言葉は、わかりにくいかもしれません。私たちは、言葉に戸惑いました。 しかし、200人が全生徒数ですから、分数で云えば分母になります。これが1単位のことです。 比較量（割合に当たる大きさ）という言葉にも戸惑いましたが、女子の人数の割合を問う問題ですから、女子80人が分子になります。

分母の200と分子の80を、分母が1になるように200で割ってやったのが答えになります。 学習指導の助言を見ます。

家庭でお子さんに教える場合、言葉のギャップを理解しないで教えるとお子さんは混乱する可能性があります。 しかし、指導要領との違いを認識した上で指導すれば、正答率が57%ということにはなりません。 分数問題にして教えれば、混乱もなく点数も良くなると思います。そこで、誤答の理由も推察しなければなりません。 80％と答えた7%の子は、多分、%を出す問題だから女子生徒数80を100で割ったと推測します。0.4％と答えた11%の子たちはかわいそうです。割り算はできているのに100倍するのを忘れたか、知らないかのどちらかです。 22.6％の子たちです、問題は。 比や割合を分数の問題とせず、比較量、基準量という大人でも混乱するような言葉で指導することにも課題があるような気がします。 算数ができないのは読解力がないからだという人が多いです。文科省にもその傾向があります。 C言語をあきらめたという仲間の一人は、高1で因数分解を習ったとき、因数という言葉の意味がわからなくて一学期棒に振ったと嘆いていました。因数のために頭の方が分解したと笑っています。 算数や数学の用語は極めて難しい上に、親切心からと思いますが、やたら読む量が多い出題の傾向になっています。 小学生の算数は、数の論理やパターンを教えて“数のセンス”を磨くのが基本です。オーストラリアの研究ですが、数の論理を理解しない子には連立方程式など無理という実証試験があります。 用語の定義を正しく教え、比や割合は分数の問題として一貫性を持たせるようなことも必要と思います。 関係者のみなさんが分数教育に努力されている二つ目の例を紹介します。 岡山大学大学院教育学研究科の黒崎東洋郎氏が、2015年の岡山大学算数・数学教育学会誌『パピルス』第22号に「アクティプラーニングに基づく算数の授業改善」と題した論文を発表しています。 この論文は、分数学習の早い段階で比を教えなければならないのではないかと思わざるを得ないヒントになりました。 黒崎氏は、「分数のかけ算の意味を理解する学習となると、なかなか困難な課題」とおっしゃって、その困難さを「塀の板をlLのペンキでは2/3m2塗れるそうです。このペンキ4/5Lでは、何m2の壁の板を塗ることができますか」という具体例を挙げて説明されています。ちょっと大変かと思いますが、以下の引用をお読みください。 『数量が既習の整数や小数のかけ算の場合と閉じように考えて、式2/3×4/5と、分数のかけ算の式に表すことは子どもにとって簡単ではない。第6学年の分数のかけ算の意味理解の指導上の困簸さは、学習経験の深い「基準量のいくつ分」という既知の理論値が通用しないところである。子どもにとって大きな学習障害となり得る場面である。つまり、分数のかけ算の立式の根拠は、単項演算(倍概念)を根拠にしなければ説明できないので、倍概念の理論知が必要である。ペンキ4LはlLの4つ分だから、塗れる面積は2/3m2の4つ分だから2/3×4と「基準量のいくつ分」を根拠にすればレトリックのある説明となる。しかしながら、ペンキの量が4/5Lの場合では、「基準量のいくつ分」の考えは通用しない。「基準量のいくつ分」のという考えは、「いくつ分」は整数で表現できるので、整数の場合には通用する。けれども、かける数が分数になると、「いくつ分」を整数で表すことはできない。 分数のかけ算の意味を説明するには、「基準量のいくつ分」から「基準量の何倍」に思考・表現する思考・表現する数学的アイデアを方向転換する必要がある』。すなわち、子どもは苦手な単項演算に基づいて、「基準量何倍」と考えて、帰納的・演樺的に考えて、説明する必要がある。具体的には、lLと4/5Lのペンキの数量関係から4/5Lは、lLの4/5倍という倍関係を見いだし、もう一方の1Lペンキで塗れる面積と4/5Lでぬれる面積の数量の依存関係に着目し、依存関係にある2つの数量の比例関係で演算決定できることを、下記のような図を使って説明する必要がある』と次の図を示します。

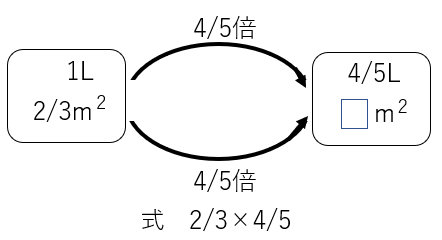
さらに、『このように、かけ算が用いられる場面を分数に拡張する場合、かけ算の意味をどのように主体的、協働的に子どもに合意形成を生成すればよいか、深く考えて探究すべき課題が存在する。すなわち、どんな計算になるのかなと疑問を生成し、まず、分数のかけ算の式に表したら終わりではない。次は、なぜ、かけ算の式に表せるのか、その理由を探究していくのがアクティプラーニングである。分数のかけ算には、さらに、分数同士のかけ算の仕方についても深く考えるべき課題が存在する。計算技能のマニュアルとしては、下記の通りである』とおっしゃいます。

（引用終わり） https://ousar.lib.okayama- u.ac.jp/files/public/5/53719/20160528121832588384/papyrus_022_083_090.pdf かける数が分数になると、「いくつ分」を整数で表すことはできない。 分数のかけ算の意味を説明するには、「基準量のいくつ分」から「基準量の何倍」に思考・表現する思考・表現する数学的アイデアを方向転換する必要があるという表現がありました。 この最初の行のかける数が分数になると、「いくつ分」を整数で表すことはできないというのですが、整数で表す必要はないと思います。 ここまで散々述べてきたかける分数の分母と分子の論理の話です。

整数は、1、2、３，４・・・という自然数のことでマイナスも含みます。小数点のある小数は整数ではありません。分数は割り算ですから少数になる場合があります。黒崎氏は、それをおっしゃっていると思いますが、上の図に少数など出てきません。分数は、そういう意味で便利な道具です。便利な道具というのも教えたらいいと思います。道具は使うものです。分数に使われるのではなく、道具として使う。掛ける分数の分母と分子の意味さえわかれば、整数になる、ならないに悩む必要はありません。悩みがなくなれば、少しは不安も解消すると思います。悩み解消比に移ります。比を習っていれば1平方メートルに必要なペンキの量が1.5リットルとわかるので、話がうんと簡単になります。

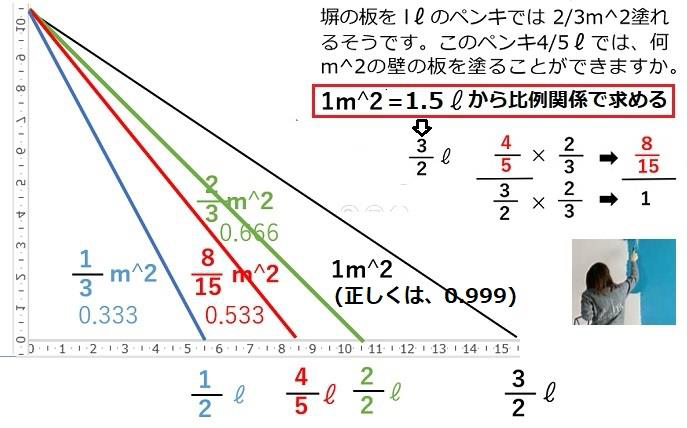
4/5リットルを3/2リットルで割る分数の形にして、分母を1にしてやるだけです。

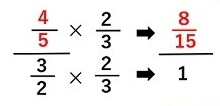
そうすると分子が8/15平方メートルになり、それが答えです。

分数が便利というのは、グラフに記入した分数と少数を見ればわかります。1平方メートルの1は整数です。3分の1平方メートルを3倍すれば1ですが、少数の計算では0.333平方メートルを3倍しても１にはなりません。ですから、分数のまま計算すればいいのです。再び、比を教えるタイミングの問題です。分数で、分母と分子に同じ数を掛けても、同じ数で割っても同じというのは習います。それは、比が同じということですが、2年生では習いません。家庭対話の教え方次第ですが、子どもの負担にはならないようにはできます。そうなれば、割合問題を分数の問題に転換する指導はできます。そこで、はじめて分数、比、割合の指導に一貫性が生まれます。成績も確実に上がると思います。 黒崎氏の論文は2015年の公開です。2012年に大幅な教育改革が施行されました。 黒崎氏の論文は、改革を真摯に受け止めているのが伝わってきます。それ以上に、現在の教育の流れを知る貴重な情報を与えてくれました。感謝します。

2012年の教育改革と2018年の新しい社会5.0は連続しているもので、世界の流れに沿っています。国際団体ATC21sのスキル養成に呼応するものです。世界的に見ても教育格差は拡大しており日本もその傾向にありますが、2018年のお茶の水大学の調査研究によれば、例え、家庭経済が厳しくとも子どもたちが頑張っている姿が目に浮かびます。近いうちにシリーズの別項で取り上げます。21世紀が求めるスキルとは何かを見ます。

驚くなかれ、小学生にまで批判的思考やメタ認知力を求める教育になっています。想像力とイノベーションの思考の方法を育むのです。お亡くなりになった故千葉博士のご本を思い起こします。

故千葉康則博士のおっしゃった子どもたちが生来的に持つ「好奇心と探求心」を伸ばしてあげなければならなければ、想像力もイノベーションも起きません。 算数不安症に悩めば、批判的思考どころではありません。 自分を突き放して心を探るメタ認知力も不安に覆われるだけになります。 私たちも決して偉そうには云えません。たまたま、一年前にある“きっかけ”があったので、文科省の指導要領や学力テストを調べることになり、算数不安症を知っただけです。 “きっかけ”がなければ、多くの大人と一緒で、21世紀スキルも知らなかったと思います。分数の教え方に一貫性がないかもしれないということに気付くこともなかったと思います。学力テスト問題がどうなっているのかも知りませんでした。 大人として怠慢でした。 反省の意を込めて、「割合と分数」の学力テスト問題を二つほど一緒に考えたいと思います。 リボンの価格問題。正答率47％。

右の画像は、ここまで説明してきた分数の論理に従って処理すれば案外簡単かもしれないという指摘です。後ほど触れますが、その前に、何が原因で誤答が生じたかを検討します。 0.6mの代金と答えた誤答の子が13%。0.6で割ったから、そう考えた訳です。 6mと答えた誤答は、10倍したのを6で割ったからです。22％の誤答は大きいです。 10mと答えた子が、どうしてなのかわかりません。 大人が持たなければならない読解力とは、間違って答えた子たちが、何を考えてそうなったか考える力のことです。できた、できなかった、だけでは何の解決にもなりません。 小説読むのだってそうです。偉人伝読むのだってそうです。書き手の頭の中を読む。それが、読解力です。21世紀に必要なスキル、リテラシーそのものです。 概念や論理を教えないで、テストの点数だけの教育システムが悪いと批判するのは簡単です。しかし、先生方も懸命の努力をしています。しかも、5000年前からの数学の進化の歴史が今に凝縮しているわけですから概念や論理を教えるのは容易なことじゃありません。そこで、リボン問題指導が概念を教えているかどうかを検証しなければなりません。

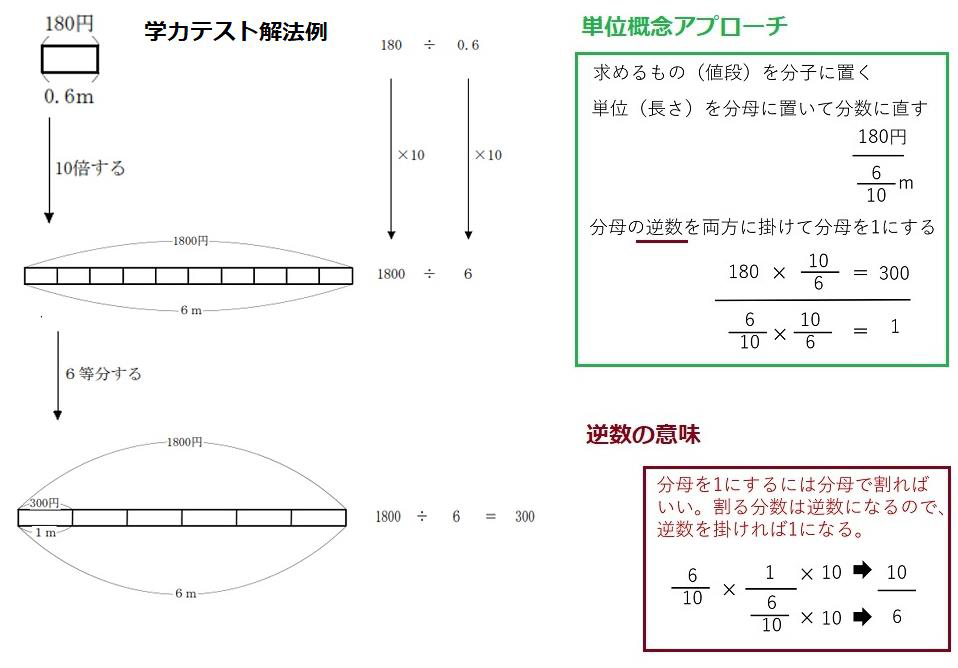
ものすごく苦労して教えようとしているのがわかります。この解法例は、1単位を10等分して、さらに6等分する。1単位という概念はあるようですが、10倍して6等分するというのには、多分、子どもたちは混乱すると思います。 右画像の説明をします。このリボン問題は、分数の問題として捉えれば簡単です。 リボンの長さと値段が比例関係にあるので、単位量（0.6m）を分母にとって180円を分子に置く。分母の0.6mを1m（これが1単位）に変換すれば、分子が答えになります。 分数の逆数の意味もきちんと教えてやる必要があります。逆数を掛ければ1になるのを知っている子はいるはずですが、逆に、1単位を与えられた分数で割ってやれば逆数になるという計算は多分知らないと思います。下の左の分数計算です。

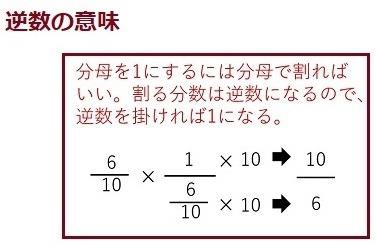
右の図を見ながら説明します。1単位というのがオレンジ色の囲ったものです。6/10に逆数10/6を掛けるのは、6/10を6分割して10個足すことですから1単位になります。左は、6/10の逆数を出すのが左の計算です。どんな分数でもいいのですが、1単位を与えられた分数で割れば逆数になる。小学生に単位概念を説明するのは難しいと申しましたが、やっぱり難しい（笑）です。要するに、分数というのは、あくまでもオレンジ色の枠内のことと考えたら気が楽になるかもしれません。帯分数というのも基本は同じです。

分数の足し算や引き算で分母を同じにする通分というのも低学年性が苦手と云われます。最小公倍数で分母を同じくするわけですが、確かに面倒です。しかし、通分をどうやるかは学校で習うので、九々をきちんと覚えるぐらいしか云えません。しかし、1単位を細かく分割して「均等に詰めてやらないとならないから」というような単位概念を持ち込めば少しは役に立つと思います。ぜひ試してください。 また、1単位に収まり切れるか、収まり切れないかというのは、単位概念を理解する助けになると思います。 かなりややこしい話になりましたので、再び気分転換したいと思います。 ホンダカーズ川崎中央宮前平店のガラス窓に素晴らしい言葉がありましたので、思わず写真を撮りました。本小論に掲載するのを快くお認めいただきましたので、みなさんと共有したいと思います。

ホンダカーズ川崎中央宮前平店 〒216-0005神奈川県川崎市宮前区土橋2丁目11-1

もう一息です。 同じ数で割ってやれば1になるというのは、整数で知っていても、分数でも同じと知っているかどうかわかりません。分子・分母がさらに分数を含むような分数を繁分数と呼びますが、改めて云うのもなんですが、こういう分数です。

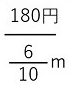
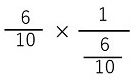
小学低学年では習わないと思いますが、家庭では教えた方がいいです。小中学生レベルでは、分数をそのまま数字として使って一向に構いません。 私たちがそう云っても疑いを持つ方もいらっしゃると思いますので、ご一緒に確認しましょう。 数学用語は難しいので、うんざりしますが、実数という用語があります。ウィキペディアの定義を引用します。 実数とは連続な量を表すために、有理数を拡張した「数」の体系である。 今度は有理数。 有理数とは、二つの整数a,b（ただしbは0でない）を用いてa/bという分数で表せる数のことをいう。 そして分数。 分数とは2つの数の比を用いた数の表現方法のひとつである。 念のために、有理数でないものを無理数と云いますが、その無理数。 無理数とは、有理数ではない実数、つまり分子・分母ともに整数である分数（比）として表すことのできない実数を指す。 いかがですか。 分数を分数として、そのまま使って良いのです。数の論理が整数と同じになるのでずいぶん楽になると思います。分母と分数に10を掛けてやらなくとも、分母と分子が同じですから1になる。割合を克服するために分数を大いに使えるようにした方がいいと思いますのでくどくど説明しました。

お疲れと思いますが、最後に、正答率17.9％のリサイクル問題で終わりたいと思います。

生徒の肩を持つわけではないですが、棒グラフは間違いやすいです。視覚の問題が絡みます。正答は、1の「ペットボトルの重さの割合は、4月ほうが大きい」ですが、棒グラフを見ると目に残りやすい黒色が4月から6月まで同じです。 正答の子の中には、いきなり分数に転換している子もいると思いますが、グラフを見たとたんに生徒の頭の中に分数が浮かび上がるような指導をしてくださるよう先生方にお願いしたいと思います。 4月 20kg/80kg 5月 20kg/90kg 6月 20kg/100kg 引用、及び、参考にした資料の一部を列記して、シリーズ（1）を終わります。 お読みいただき、ありがとうございました。

シリーズ（1）完