
数の論理なんていうから、どんなに難しいことかと思っていたのだけど、あの分数の掛け算の説明読んだら、「えっ、こんなもんが論理かと気が楽になりました」と 81歳の町山さん。
シリーズ1の分数の説明のことです。
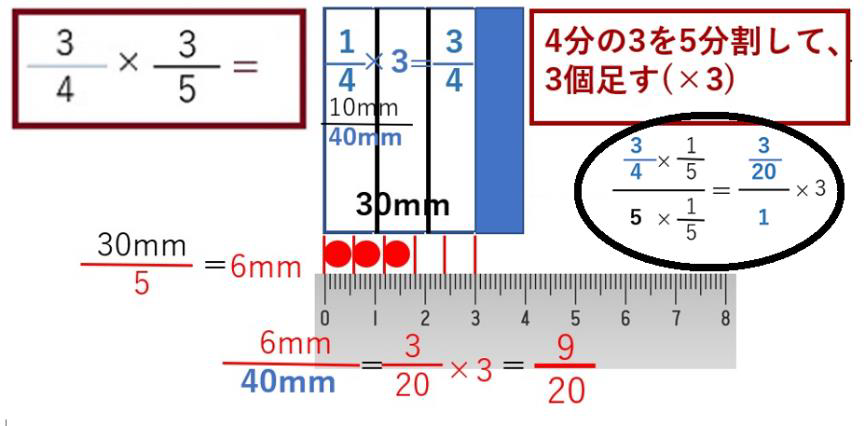
「4分の3を5分割して3個足す」なんて説明聞いたことがなかった上に、黒丸内の計算順序で、分母同士、分子同士をかける理由もわかりました。こんな簡単なことだったのかと気が抜けたとおっしゃる町山良行さん。明治大学柔道部出身。講道館認定六段。
社会人になって間もなくイタリアはじめヨーロッパ数か国を訪問したといいます。今から60年前に海外旅行を経験した人は極めて稀です。1959年(昭和34年)の現上皇陛下と上皇后美智子さまのご成婚。ご成婚記念として総務省が国際交流のために青年派遣団を結成したそうです。町山さんは、第8回の派遣団に選ばれた一人です。イタリアでの写真があまりに素敵な笑顔なのでお願いして公開に同意いただきました。
子どもは国の宝とおっしゃって算数不安解消プロジェクトに参画しました。

そして、「この程度が論理なら頭の体操にいいから、お孫さんを持つ同年輩にも教えたい」と考え出したのが、「数の論理テスト」5 問。
「ああ、こりゃダメ。難しすぎる。みんな算数というだけでそっぽ向きます」と慎重な物言いの有志代表。農芸化学出身 櫻井由和さん。茨城県出身。

日本民家園のある川崎市生田緑地地域を元気にするための住民交流会「カメぱっぱ」の主宰者です。「今はね、認知症防止とかでいろんな脳の活性化ゲームがある。最近話題になっているのが囲碁。東北大学の教授も推奨している。女医飯塚あい先生が、囲碁協会のサイトに寄稿しているので読んでごらん。」


飯塚あい氏は、埼玉医大卒で「囲碁を認知症予防、高齢者の生活向上や介護予防に結び付けたい」という志を持って東京都健康長寿医療センター研究所に勤務されておられます。


「碁は確かに頭を使いますね。大学の先生がいつまでもお若いのも常に考えているからなのでしょうね。だけどね、櫻井さん。難しいといっても小学生の算数ですよ。教え方次第というのは分数でわかりましたよね。認知症云々は別にして、老人になると寂しいのはわかるでしょう。孫にもそうそう会えるものでもない。しかも、私たちがやろうとしているのは、算数恐怖症解消です。学校で教えない数の論理教えて・・・」
論理ときたか、町山さん・・・で?
「学校で教えない方法教えて孫の成績が良くなったら生きがいになるでしょう。心が燃えるでしょう。英国で成人の算数不安症が社会問題になっています。日本も同じでしょう。大人が自分の不安を解消できずに、どうして子どもの不安を取り除けますか。子どもだけの問題じゃないです。シリーズ1を読み直してください、櫻井代表。」
シリーズ1:http://kamepapa.com/math/
代表、黙っちまいました。
5秒後、「じゃあ、聞こうじゃないの。どのように教えるのか、 一番目から順序良く、本番のようにやってください。」
俄然張り切った町山さん、意気揚々と話し始めました。
第一問

答えはこれです、これ。

学校じゃなかったと思うけど、だれかに教わった記憶があります。頭のいい人がいると思いました。実は、私が知っているくらいですから、日本人全員みんな知っていると思っていました。ところが、知らなかったという人に最近出会いました。三人が、三人とも知らなかった。一緒に話していた時ですけど。
知っている人は多いとは思いますけど、これが奇数になると思いつかない人は多い。

私は、高校数学レベルの数学は全然わかりません。数列というのもある。しかし、奇数の足し算を知っていた方がいいと思います。
「う.ん、数列か。私も得意とは云えなかったけど、使い道があるのかな」と櫻井さん。
バカにしちゃいけませんよ。自慢じゃないですけど、この奇数列足し算のお陰で数学苦手の私が、早稲田大学の数列問題解けました。丸二日間掛かりましたけど。
その内、「どうして私が早大に」というタイトルで苦難の二日間を書きます。中学の算数で大学入試までやれるという実証にしたいと思っているので、ちらっとだけお見せします。

元数列の項数を求める公式など知りませんから、下の表を作って何時間も眺めて、ああでもないこうでもないと観察して“数の関係”を発見しました。パターンというのかな。

ここから方程式みたいなものを導き出したので問題集の解法と違いますが、論理は合っているから同じ答えになりました。苦労しましたが、お陰で数が怖くなくなりました。
まあ、楽しみにしていてください。
横道はここまでにして、第2問。この質問は、直ぐに答えが出るか知りたいだけです。

千は直ぐに出ると思うけど、1億はどうでしょうか。大きな数になるとゼロの数は直ぐに出てきません。これは、次の第3問の前段階です。算数に大事な気づきのためです。

代表、いかがですか?
「黒字がカギですね。あっ、4乗と1の後のゼロの数が同じ4個ということ?」
さすが、代表、鋭い。そうです。私のパソコンのプロセッサーが2.7GHz(ギガヘルツ)とあります。1秒間にオンオフが27億回という意味だそうです。2.7×10の9乗です。ゼロが9個つきます。
「10進数も2進数も数の数え方だから論理は同じ。数の関係をきちんとわからないで方程式はムリとオーストラリアの研究も指摘している。2進数やれば10進数の理解も一段と進むので成績は必ず良くなる」と主張する2進数オタクは正しいかもしれません。「数の関係というのはこういうこと」と見せられたこの表。数え方(進数)が違ってもべき乗とゼロの数が同じです。やっぱり2進数教える必要があるのかと思い直しました。

それと、米国では小学3年生から習うのに、日本は高1ですね。
「えっ、なに?・・・2進数?」
そうですよ。コンピュータの信号処理だから基本の基本でしょう。日本の子たちどうするつ
もりなのだって、焦りました。 算数不安解消プロジェクトに参加したのは、それも理由の一つです。負けてたまるかという気持ちです。2進数はオタクに任せて、先に進みます。
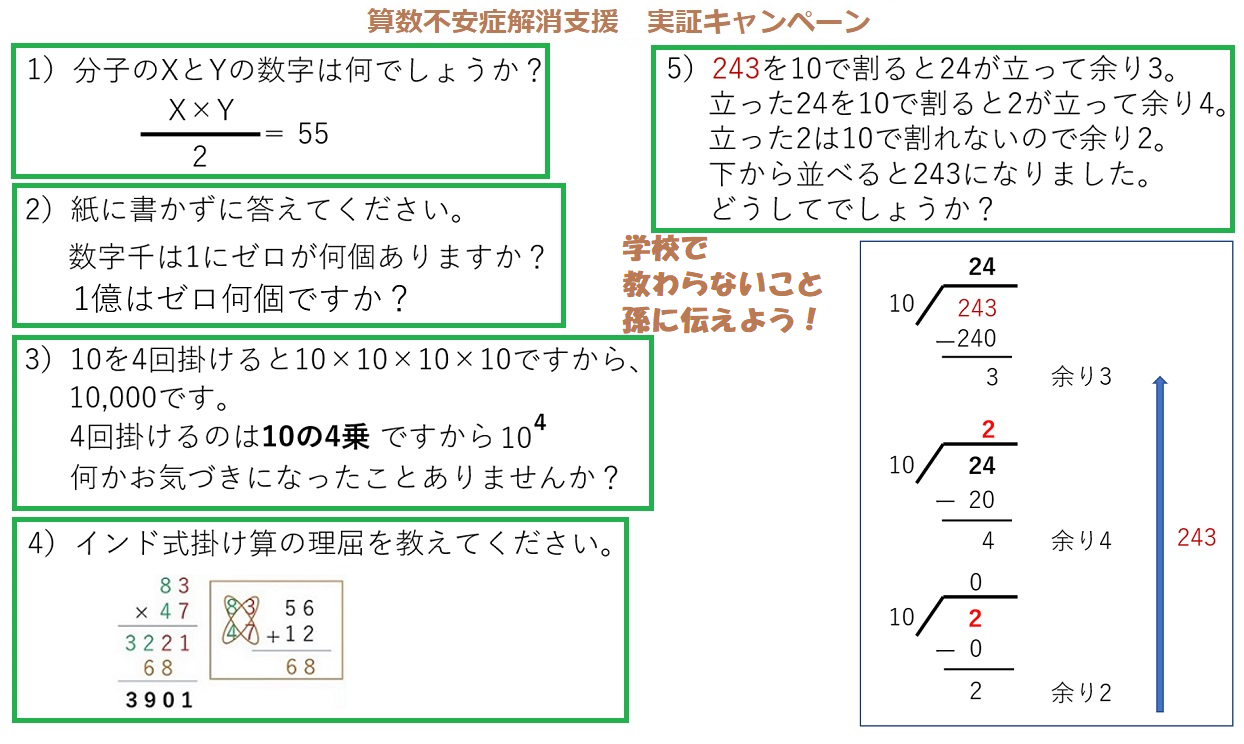
次は、第4問。インド式掛け算。
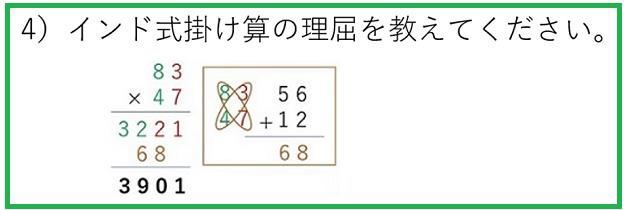
10進数は、0から9までの10個の数字の数え方なのは、もちろん小学生の子も知っています。9で桁があがって二けたの10になる。二けたが99まで続いて三桁の100になる。これをヒントにしてインド式計算の論理を説明してくださいというのが第4問。
インド式など聞いたことがないという方が多いのがわかりましたので、ヒントついでに、普段やっている方法との比較を見せようと思います。

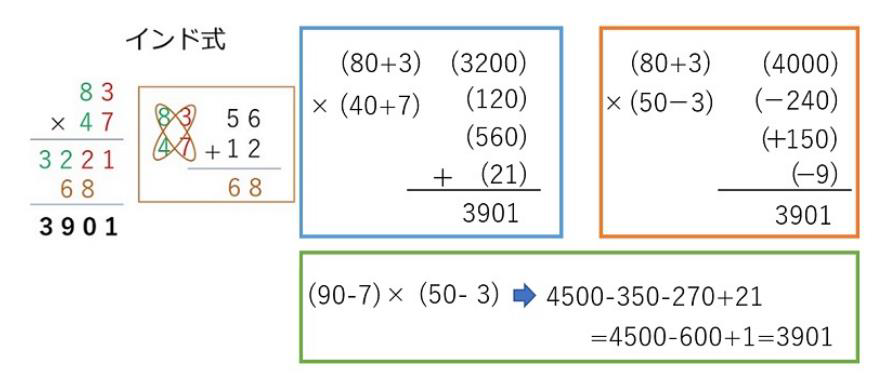
日本式の場合、まず、7×3の21とやる。頭の中で 2上がってと、7×8=56に2を足して、581にする。83 に4を掛ける場合も、シサン12。1上がって、シハ 32に1を足して33にする。実際には、右下に示したようにやっているのですが。それに対して、インド式は、一桁同士を掛けた二桁の21をそのまま書く。二桁目の数8と4は、80と40ですから、掛けた 3200の32を21の前に書いて3221と置く。次に、斜め掛け算した56と12を足した68を3221の三桁目と二桁目の下に置いて足し算する。
どっちがいいということではありません。ただ、明らかにやり方が違います。
その違いを理解することが重要です。
インド式は、83を(80+3)、47を(40+7)と分解して(80+3)×(40+7)という掛け算をしているのが違いです。
{(80×40)+(80×7)+(3×40)+(3×7)}=3200+560+120+21=9801
お孫さんに説明するときには、次のように説明したら良いと思います。
最大値と最小値という考え方。桁の意味がわかるようになります。

さらに、二桁同士を掛けても決して五桁にはならないというのを教えてやってください。
二桁の最大値同士、99×99をインド式計算したのが右にあります。片方が、三桁の100でも五桁になりません。100同士になって、初めて五桁10,000になります。
実は、櫻井代表。桁が大きくなると処理できなくなる小学生も多いのです。 インド式掛け算を持ち出した理由がそこにあります。
かなり前のことですが、公園で遊んでいた中1の男の子5人と女の子2人に、新しく導入されたプログラミング教育について尋ねたときのことでした。
周りが、「算数はこの子が一番」という男の子に、「どんな数字でもいいのだけれど、10で割りきれない場合、余りはいくつになるかな」と尋ねてみました。
じ〜っと考えて、「11のときは、1が立って・・・」とぶつぶつ呟いたので、恥かかしちゃ拙いと思ったので、慌てて話題を変えました。
「じゃあさ、クラスの子たちは二桁の掛け算はできるのかな」と聞くと、できる子もできない子もいるという答え。「じゃあ、三桁の掛け算は」と尋ねると、男の子一人と女の子の一人が即座に、三桁はできな〜いという回答でした。
元々、「10で割り切れないときは、余りは1から9のどれか」という答えが直ぐに出てくるかと期待した質問でした。
ところが、7人いる子の誰も何とも云わないので、若しかすると、小学生段階で、10進数の性質をきちんと理解している子は少ないかもしれない。桁の理解も十分じゃないかもしれないという疑問が湧いたのです。
それで、その後、中学生と高校生20人以上にこのような問いかけをしてみました。
「君たち、235 を 200+30+5 と分解する意識持って計算しているかな〜」と。
少なくとも7割の子たちに分解の意識がないという感触でした。この意識を持つかどうかで計算の工夫の仕方に違いが出ます。

分解すれば、括弧内の掛け算をします。その例を三つ挙げました。三桁同士もメモ用紙があればできます。

(a+b)×(c+d)= ac+ad+bc+bd という掛け算です。
実際には、日本式掛け算もこういう計算をやっているのですが、一般式という形で習うのは後です。早くに教えた方がいいとは思いますが、指導要領の関係があるのでそうもいかないのでしょう。インド式計算を持ち出した背景には、子どもたちとの会話があったのです。私自身、インド式掛け算やったおかげで分解を覚え、計算が早くなりました。99×99が、暗算でできるようになりました。

自分でも信じられないです。自分の算数不安がかなり解消しました。
文科省の指導要領でも計算に工夫を凝らすというか、様々な方法を生徒自体が考え出すよう指導はしていますので、みなさんからもお孫さんの指導にお使いください。
とまあ、こんな具合に説明しようと思っているのですが、どうでしょう、代表。 画像にちょこんと載せた足し算の発見ですが、今、哲学教育の必要性が叫ばれていますね。 数学史に出てくる偉人たちは、哲学者であり、科学者であり、数学者です。哲学は考える。科学は実証する。数学はそれを繋ぐ言語とおっしゃる人たちもいます。過去の何千年もの歴史の中で培われてきた算数ですから、教えるのが難しいとは思っていました。自分でやってみると、改めて難しさを実感しました。先生たちのご苦労がわかります。
「いやあ.、驚きました。正に、論理ですね。“数の関係”というのかな。そうですか、桁の意識が問題とは知りませんでした。これなら、小学生の高学年の算数が苦手な子の刺激になるかもしれない。老人ホームから引っ張りだこになるかもしれません。5問目が楽しみです。続けて貰えますか?」
代表に褒められたので気を良くして第5問。
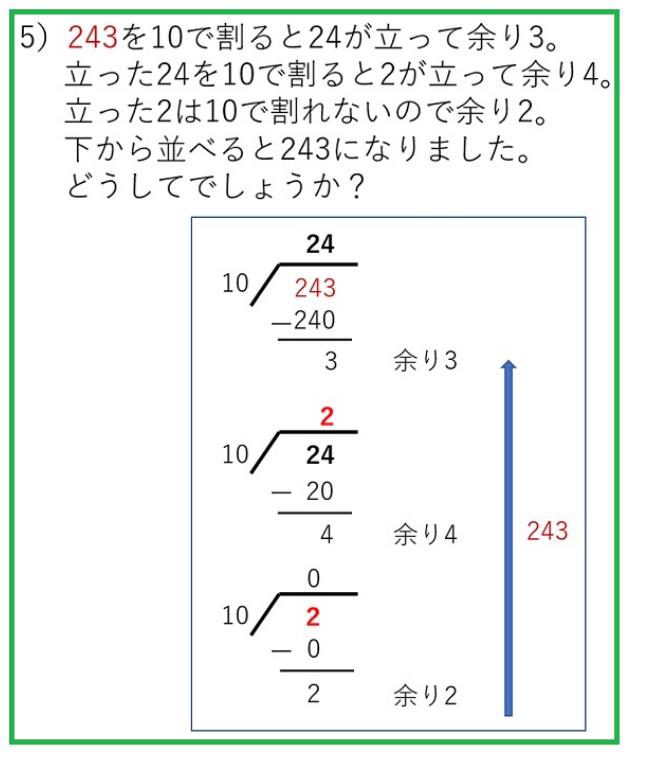
下から並べる理由と尋ねられて直ぐに答えられる人は、ほとんどいません。私も、最初はわかりませんでした。10進数を2進数に転換する場合も2で割って下から並べますが、ITパスポート国家試験合格者でも下から並べる意味を知らない人がいるそうです。
説明の仕方が下手なので、ややこしくなるかもしれませんが、こんな具合に説明します。
243 を10で割るという意味はおわかりと思います。
243 には、10が24個ある。10にならないものが3ということです。それが余りです。

逆に云うと、10を24 回足したら240になる。それに、3を足せば243です。
最初の割り算の余りは、三桁数字の一桁目です。
今度は、立った24を10で割る。どうして10で割るのかという疑問が出るかもしれません。 最初が243を10で割って余りの一桁目を探した訳ですから、24を10で割って、出た余りは二桁目というのはわかると思います。2が立って、余り4。そして、立った2を10で割るのは、三桁目の数字を探している訳です。ですから、下から並べると、元の数字の243と同じになる。
インド式掛け算で話したことですが、243を(200+40+3)と分解する意識があれば、もっとわかりやすいと思います。
(ところで、櫻井さん、ご老人の中にはできる方がいらっしゃいますから、「243を100で割れば三桁目の2になるじゃないか。どうして、ややこしい説明するのだ」という指摘があると思います。指摘があってもなくても、この説明もするつもりです。)
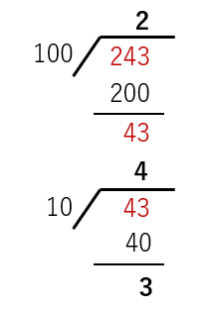
(200+40+3)の分解意識があれば、こっちの方が説明は楽です。
最初に100で割って、200の2。三桁目。余りの43を10 で割って二桁目が4。余りが3ですから、それが一桁。
下からでなく、上から並べたら243で当たり前の話になります。
なのに、どうして下からならべる話を持ち出したのか、その理由をこのように説明します。
理由は三つあります。
一番の理由は、下から並べる方法をお聞きになったことがないだろうと思ったからです。聞きなれたものを聞かされても脳は活性化しません。
二つ目の理由ですが、下から並べるのも上から並べるのも桁を探す論理は同じです。やり方を変えて、普遍的論理を理解するのは思考を柔軟に保つために必要だからです。
そして、三つ目の理由が最も重要です。お孫さんが学校で教わらない方法だからです。
学校で教わる方法をわかるように指導するのも大切です。しかし、それ以外の方法を教えると目が開く場合があります。
また聞きですが、子どもは、幼児からの成長過程の中で独自の計算方法を身に着けるといいます。数多くの研究結果から、ほぼ間違いないというのが定説のようです。折角子どもが独自に考え出した計算方法をまっさらにして、画一的な計算方法を叩き込むのは、子どもの創造性を失わせるとさえ云う研究者もいます。素人の私が、脳科学の論争に云々できませんが、算数はあくまでも数の関係ですから、論理さえ正しければ、異なる方法を示して子どもに選択の余地を与える方が良いかもしれないと思います。
そういう意図もあって、4問のインド式掛け算と5問の桁探し問題を連続させました。 計算を楽にする数の操作アイディアをたくさん紹介したかったからです。
学力テストには、例えば、このような問題が出ます。
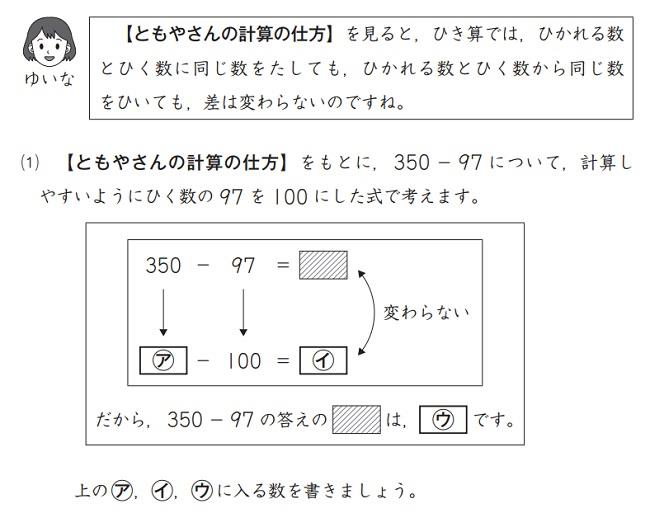
数を使いこなすアイディアがあれば、このような問題にも余裕を持って対処できると思います。
これは、極めて簡単な引き算ですが、少し複雑なものもあります。

割り算ではこういう例があります。

と、まあ、こんな調子でやろうと思っているのですが、櫻井代表、講評をお願いします。
「説得力があり、しかもわかりやすいすばらしい説明でした。こんなポスターでも作成して活動始めましょうか。」
この後は、オタクの2進数でしたね。・・・・・(お、オタク?)

オタクじゃないです、失礼な。サーフィンはやりませんが、74歳まで世界最年長ウェイクボーダーになろうと肉体年齢をちょっと忘れた変わり者というだけです。

午後のレッスンの私だけがウェットスーツに着替えていないだけです。変わり者というわけではありません。
ところで、2進数をやろうと云っても、目的は、あくまでも子供たちの算数不安症解消です。
それを忘れないでください。
ところで、町山さんのプレゼンは素晴らしいと思いました。
特に、冒頭の「数の論理なんていうから、どんなに難しいことかと思っていたのだけど、あの分数の掛け算の説明読んだら、えっ、こんなもんが論理かと気が楽になりました」というやつ。不安は心理問題ですから、気が楽になればほとんど解決です。実に良かったです。
シリーズ1に、日本の分数指導に混乱があると指摘しましたが、どうも、日本だけのことじゃない。世界が混乱しているというのをごく最近知りました。
子どもたちの数の視覚認識システムに関する研究論文の抄録集があります。
「The Object Tracking System」
https://www.sciencedirect.com/topics/psychology/object-tracking-system
この中に、子供たちがどのようにして分数を学ぶかという研究があります。米国デラウェア大学のナンシー・ジョーダンという科学教授の「Fraction Development in Children:Importance of Building Numerical Magnitude Understanding」というタイトルのものです。

ジョーダン教授は、「2013年頃までは、整数と分数は別個のものと捉えられていた。子どもたちが分数を覚えるのは整数よりず.と後のことで、しかも、整数を学ぶこと自体が分数の理解を阻害するので学習が難しいという理論が主流であった」と云います。ところが、「いや、そうじゃない。幼児であっても8と16ドットの識別をする。2対1という比も認識する。つまり、比や分数の視覚概念を持っている。数字という形で数の大きさを認識するのは年齢と共に進歩するのは事実である。多くの研究が、小学1年生前に0.10、2年生までに1.100、4年生までに0.1000を認識することを示している。子どもたちが数直線上で分母の大きい真分数、整数と分数を組み合わせた帯分数、そして、分子の大きい仮分数という順序で学んでいくという実証研究もある。つまり、子どもたちは、整数と分数を別個のものとして学ぶのでなく、数字の大きさを学ぶ全体の過程で分数も学んでいくというのが、現在の統合理論である」と述べています。
2013年頃までは整数と分数を別個のものと捉えるのが主流の考え方だったわけです。
シリーズ1で紹介した論文を読んで覚えた違和感は、ここに原因があるとわかりました。
さらに、算数不安を解消しようとしているのが私たちだけでないこともわかりました。
「これだけ多くの生徒が算数を恐れるのは何故だ」と題した記事があります。「算数というのが、いろいろ探求できるアイディアの組み合わせなのだというのを生徒がわかれば、算数不安はなくなり成績も良くなる」とスタンフォード大学のボーラー教授がおっしゃっています。表紙の英文の意味です。
Why Are So Many Students Afraid of Math?(April 8,2017 Updated April 17,2017)
https://www.edutopia.org/discussion/why-are-so-many-students-afraid-math

ジョー・ボーラー教授もシリーズ1で紹介したOECDの算数不安報告書を丹念に分析してこのようにおっしゃっているわけです。私たちより4年も前です。
2017年3月に公開した「もう算数不安の時間を止める時だ」という元の寄稿文がこれです。
OPINION: It’s time to stop the clock on math anxiety. Here’s the latest research on how
https://hechingerreport.org/opinion-time-stop-clock-math-anxiety-heres-latest-research/
ボーラー教授、ありがとうございます。
私たちの背中を押してくれるようで励みになります。ご専門家から“数の関係”がわかれば成績も良くなるという声を聴きたかったのです。安心しました。
尚、表紙に用いたボーラー教授の写真は、スタンフォード大学の経歴サイトのものです。
https://ed.stanford.edu/faculty/joboaler
2進数を紹介するシリーズ3の目的も、学校では不足しがちな“数の関係”、つまり、“数の論理”を対話に取り入れて子供たちに自信を持ってもらうためです。
現在は、一方的に教える過去のスタイルから生徒同士のディスカッションで自ら学ぶというアクティブラーニングと呼ばれるスタイルに変わっています。できる子だけが盛り上がっているに過ぎないという批判もありますが、良い方向に向かっているとは思います。
シリーズ3で詳しくやりますが、正直に云えば、小学生の算数は決して易しくはないです。教える方も教わる方も大変と思いました。
5年生で躓くのは割合ばかりではありません。少数の掛け算、分数の割算もといいます。
神奈川県横須賀市の小学校の先生が行った躓く原因を探る研究があります。報告書にある躓く問題の例です。

7.2×2.4など見ると大人でもドキッとします。小数点をどこに置くかがわからない。
どうやって教えたらいいか考えてみてください。難しいと思います。
さらに、仮分数を7で割るという問題。計算はできるでしょうが、7で割るという意味がわかるでしょうか。
どう計算すれば良いかを教えるのを手続き(procedural)指導と呼んでいます。そこに重点を置いた伝統的な算数教育から、なぜ、そのような計算方法を採るのかという理由を学ぶ指導に変えなければならないというのは世界の風潮です。
算数教育に構成主義(Constructivism)アプローチというのがあります。構成主義は哲学の認識論からきたものです。20世紀の心理学に最も影響力が大きい一人といわれるスイスの心理学者、ジャン・ピアジェ(Jean Piaget)博士の0.2歳児から始まって7.11歳児に至る段階的認知力獲得過程研究はよく知られています。構成主義の意味は、「知識は他の人から直接与えられるものでなく、個々人の心の中で形成される」ということで、現在のアクティブラーニングもその影響によると思われます。
構成主義算数指導を熱心に薦める研究者の小論文によると、伝統的指導法との違いはこういうことと云います。

この例は、マサチューセッツ工科大学のメディアラボ出身の優秀な三人のエンジニアの小論文から引用したものです。
「Numerical Mechanisms and Children’s Concept of Numbers」
http://alumni.media.mit.edu/~stefanm/society/som_final_natalia_aggelos_stefan.pdf
この例が構成主義算数指導なら、町山さんのインド式計算の説明こそ高度な構成主義指導ということになります。
ここで、シリーズ3で紹介する2進数と“数の関係”について若干説明して予告編にしたいと思います。
コンピュータの信号処理が1ゼロなので、基礎の基礎を知るためでもありますが、算数の成績が良くならなければ、2進数母子対話など薦めません。
メリットを知っていただきたいと思います。
1と自分自身でしか割れない数字を素数と呼びます。2は最小の素数です。

素数ばかりではありません。4は2+2ですし、6は2+2+2です。つまり、1と2ですべての数を表すことができます。
3は奇数なので2とは異なる特徴を持っていますが、2と3という小さな素数の特徴を知れば、「数の関係」がよくわかるようになります。数が怖くなくなります。
算数を学ぶことは論理的な思考を養うためと云われています。その通りと思います。
公式を使いこなせる子が論理的と云った高校生もいました。プログラミング教育も論理思考を育むためですが、有識者会議の議論のとりまとめが以下のようになっています。

小学生の場合は、パソコン操作を指導するわけです。
「数の関係」を知るのは論理思考そのものですが、「数の関係」というのを端的に、具体的に説明します。
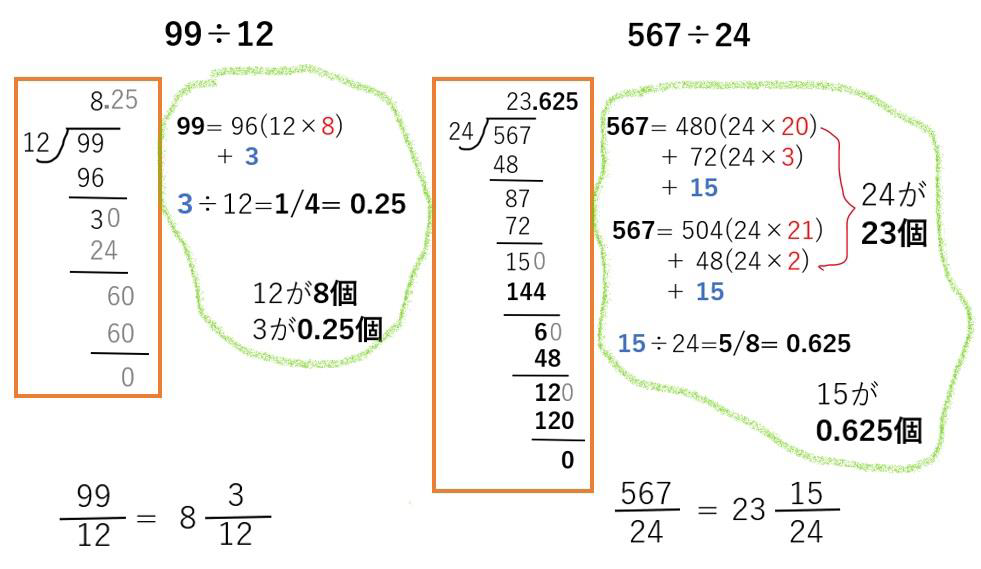
この二つの割り算は、三ケタ割る二桁がわからない5年生の指導には、3年生まで遡って二桁同士の割算を指導し直さなければならないという研究報告にあるものです。
割られる数99と567を分解するのが、「数の関係」を知ることです。

そして、割る数の12と24が、分解した割られる数の中にどのように存在するかを知ることが「数の関係」を知ることです。
分解してもバツ印をつけた数字は、12、或いは、24の倍数ではありません。それが、「数の関係」です。
12と24の倍数は、2倍ずつ、或いは、3倍ずつでもやれますが、計算上は、2倍、4倍、8倍とする2が簡単です。
伝統的な割算は難しいので、「数の関係」に重点を置けば、指導方法が変わるかもしれません。該当する子には母子対話でご指導ください。
2進数を覚えた方が良いという理由の一つがここにあります。分解するアイディアを助けます。
また、素数3の「数の関係」を知ることも大切です。

町山さんの講義にあった奇数列の合計ですが、奇数列の第一項は1です。第二項が3で以下に続いて第十項が19です。1から19まで足すと100になります。第十項、10の二乗です。項数の二乗になります。しかし、1から順の自然数ではこの法則は成り立ちません。
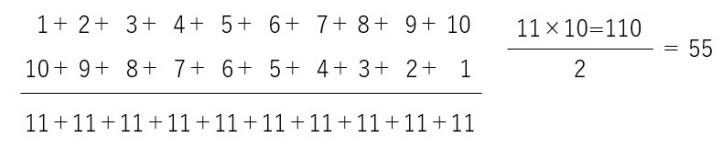
2から連続する偶数の場合でも奇数列の法則は成り立ちません。こういうことが「数の関係」です。奇数列は、3を知るシリーズ4で詳しく検討します。
2進数を学ぶメリットの一つは、得意な数を増やして大きな数字の分解や計算を容易にできることです。2の倍数が直ぐにわかるからです。半分、半分になる少数も簡単に覚えられます。
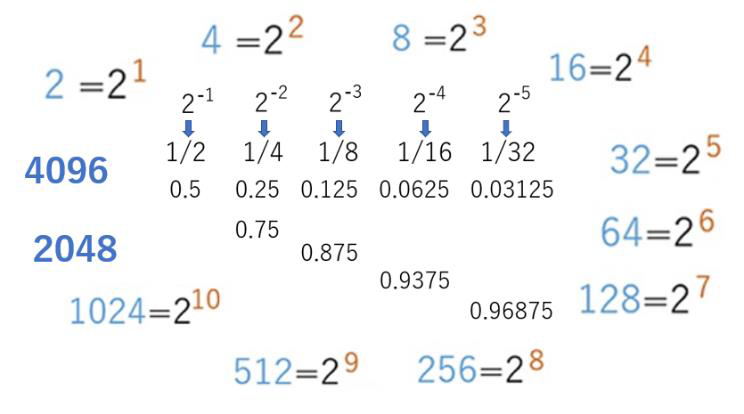
例えば、64×32という掛け算問題があるとします。暗算で、こういうことができます。
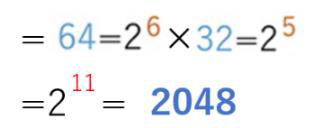
数字を分解できる子なら、2進数を使わなくてもほとんど暗算でできる筈です。
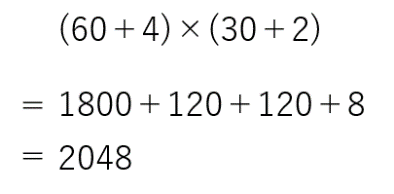
5を得意とする子なら、75×65を分解して左の掛け算も暗算でできます。2進数でやるのが右です。
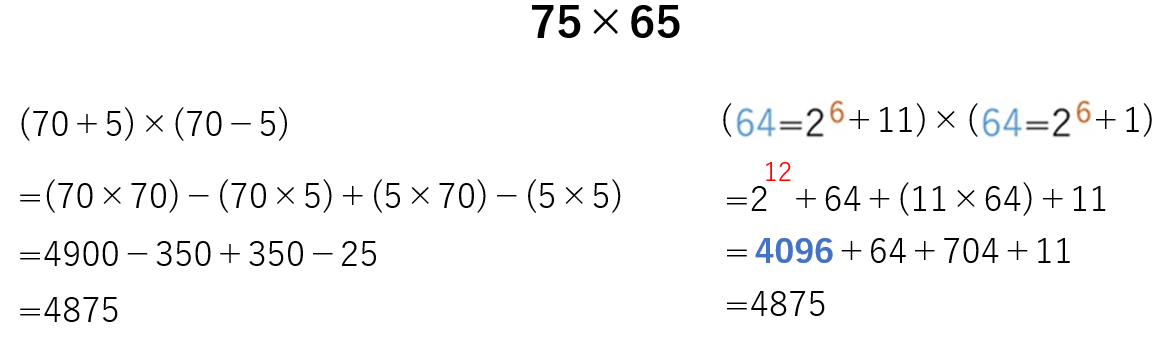
システムエンジニアの若い米国人が、「小学生の時から10進数、2進数、16進数を知っていたので計算は早かった」と云っています。
2進数をやると、得意な数がうんと増えます。何よりも、問題に対するアプローチの方法が増えますので、計算に余裕が持てます。得意な数が増えて計算に余裕が持つことができれば、数字に対する取り組み方や考え方に柔軟性が増します。正に、ボーラー教授のおっしゃることです。ここまでくると算数ばかりじゃなく、他の科目に対する取り組み方も確実に変化します。勉強そのものに不安が少なくなると思います。
日本文化のおかげで一本締め暗唱法というものを考案しました。2進数を簡単に覚える方法です。この考案がなければ、算数不安解消プロジェクト推進に自信が持てなかったかもしれません。ここに至った経緯もシリーズ2でお話しします。

それでは最後に、2進数とコンピュータの信号処理をわかりやすく説明した米国の教育財団グッドウィルの「eラーニングサイト」の記事を原文と日本語訳で紹介します。
Throughout history, almost every civilization has used a decimal number system with 10 digits: zero through nine. All of the numbers we can possibly think of use some combination of these 10 digits.
歴史を通して、ほとんどすべての文明は、0から9までの10桁の10進数システムを使用してきました。私たちが考えることができるすべての数字は、これらの10桁の組み合わせです。
Computers, however, operate differently. Instead, they use a number system that has just two digits: one and zero. This system is called binary, and your computer uses it all the time.
しかし、コンピュータを動かすのは10進数ではありません。1と0のたった2桁の記数法と呼ぶシステムです。このシステムはバイナリ(2進数)と呼ばれ、コンピュータは常にこれで動きます。
Computers need information in order to do what they do. This digital information, or data, is made up of something called bits. Bit is short for a binary digit, meaning each bit is really just a single number: either a one or a zero.
コンピュータが命令を実行するには情報が必要です。必要とするデジタル情報、またはデータは、ビットと呼ばれるもので構成されています。ビットは(英語の)バイナリデジット(2桁記数)の略で、それぞれのビットは1または0のいずれかの数値だけです。
These bits can be combined to create larger units like bytes, megabytes, and so on that we use to measure our files. The larger a file is, the more bits it has. So something like a high-resolution video is actually made up of millions and millions of ones and zeroes.
これらのビットを組み合わせて、バイトやメガバイトなどのより大きな単位を作り上げ、沢山の情報ファイルの識別に使います。情報ファイルが大きいほど、より多くのビットが含まれています。つまり、高解像度ビデオのようなものは、実際には何百万、何千万もの1と0から作られています。
But how exactly do these ones and zeroes come together and allow a computer to function? Let's think of binary like a light switch. Imagine that a one represents the light switch being on, and a zero represents it being off. With binary, the light is either on or off, with no other possible states.
それでは、これらの1と0がどのように組み合わされて、コンピュータが命令を実行するようになるのでしょうか。バイナリを電灯のスイッチのように考えてください。1が電灯のスイッチがオンになっていることを表し、0がオフになっていることを表すと想像してください。バイナリの場合、スイッチがオンまたはオフのいずれかであり、オン、オフ以外の状態はありません。
These bits are strung together as different combinations of ones and zeroes, and they form a kind of code. Your computer then rapidly processes this code and translates it into data, telling it what to do.
これらのビットは、1と0のさまざまな組み合わせとしてつなぎ合わされ、一種のコード(コンピュータが理解する言語)を作ります。コンピュータは迅速にコードを順序通り処理してデータに翻訳して、次に実行すべきことを指示します。
You might be wondering why computers use binary instead of the decimal system we use for counting things in our daily lives. As mentioned above, binary has two states: off and on. If computers were to use the decimal system, there would be 10 states instead and they would have to work a lot harder to process them all. Binary is easier for computers to process, and it also takes up less space.
私たちが日常生活で物を数えるために使用するのは10進法ですが、コンピュータがなぜバイナリ(2進数)を使用するのか疑問に思われるかもしれません。これまで述べたように、バイナリにはオフとオンの2つの状態しかありません。コンピュータが10進数を使用するなら、バイナリの2つの状態から10の状態になります。10の状態の処理は、2つの状態の処理より多くの作業が必要になります。バイナリはコンピュータによる処理が容易で、コンピュータを小さくできます。
Just like atoms make up everything around us in the real world, everything in the digital world can be broken down into binary. And even though we can't see them, it's all a bunch of ones and zeroes.
現実の世界で私たちの周りのすべてが原子で構成されているように、デジタルの世界のすべては、0と1のバイナリに細分できます。見ることができないとしても、すべて1と0の束です。
日本文は、グーグル翻訳を若干手直ししました。
ビデオもありますのでご視聴ください。
https://edu.gcfglobal.org/en/computer-science/binary/1/
教育財団グッドウィルの創設者マクレイン牧師です。

シリーズ(2)完