
2進数を母子対話のテーマにと思った元々のきっかけは、昨年暮れ(2020年)、近所の神社を訪れた帰り道、「こんにちは」と挨拶してくれた中2女子生徒三人との短い会話でした。
「君たち、2進数習いましたよね?」
いいえ、習っていません。
私の時代は、2進数を習っていませんが、コンピュータがこれほど普及した今、中学生は勿論、小学生も習っていると思い込んでいました。
コンピュータは、電気信号オンオフの組み合わせを計算する機械ですから、オンを1、オフを0で表す2進数はコンピュータの基本の基本と思っていたからです。
改訂された中学算数教科を見ても、2進数はありません。つまり、高校生になってから教わる。
参ったな~と、米国がどんな状況か調べました。全米算数教師評議会のサイトを訪れました。コンピュータ科学教師協会(CSTA)の提言を取り入れて、全米の教師に次のような指針を与えています。2012年です。9年前。
1)小学3年生に、0(ゼロ)と1からなる2進数になじませる。
2)中学3年生までに「0」と「1」を使った論理回路に慣れさせる。
3)高校1年生終了までに、2進数と16進数の関係を教え込む。
「ただならぬおもちゃ:2進数教育」とは、また、的を射たタイトルと思いますが、このサイトからPDFをダウンロードできます。
「SeriousToys:TeachingtheBinaryNumberSystem」(July2012)
https://www.researchgate.net/publication/235737801_Serious_Toys_Teaching_the_Binary_Number_System
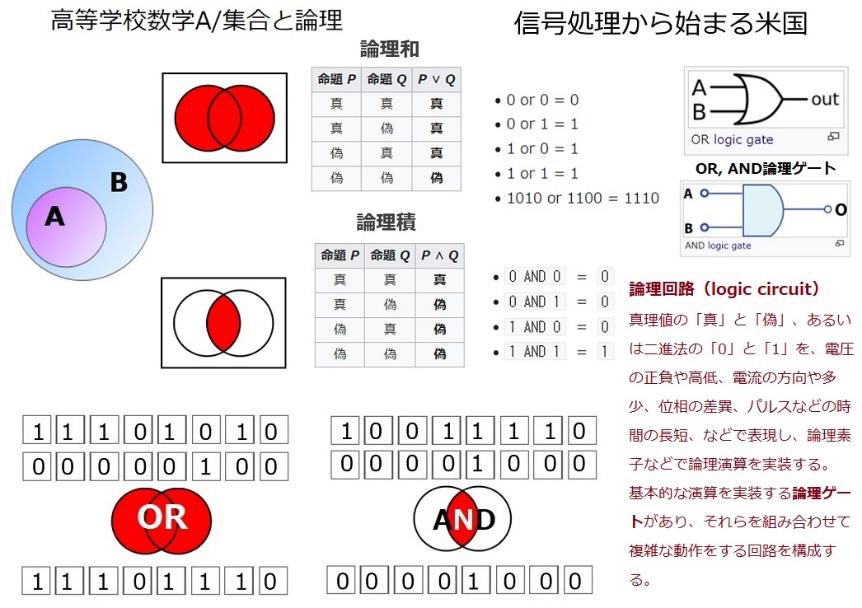
日本の指導要領では、高 1 で習う集合と論理で 2 進数を習うことになっているようです。
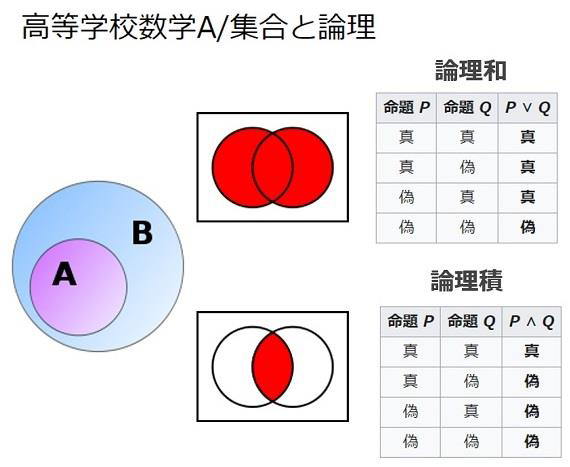
論理上の流れとしてはわかりますが、一方、小6からプログラミング教育が始まりました。文科省の目的が以下の通りです。
“子供たちがコンピュータを用いて情報を活用したり発信したりする機会が一層増えてきている一方で、その仕組みがいわゆる「ブラックボックス化」しています。有識者会議「議論の取りまとめ」(参考2(p.66))の「子供たちに、コンピュータに意図した処理を行うよう指示することができるということを体験させながら」とは、そうした情報社会に生きる子供たちが、コンピュータに意図した処理を行うよう指示をする活動を通して、コンピュータはプログラムで動いていること、プログラムは人が作成していること、また、コンピュータには得意なこととなかなかできないこととがあることを、体験を通して気付かせることです。コンピュータが日常生活の様々な場面で使われており、生活を便利にしていることや、コンピュータに意図した処理を行わせるためには必要な手順があることに気付くことが、今後の生活においてコンピュータ等を活用していく上で必要な基盤となっていきます。
プログラムを作成する上でのアルゴリズム(問題を解決する手順を表したもの)の考え方やその表現の仕方、コンピュータやネットワークの仕組み、コンピュータを用いた問題の発見・解決のための知識及び技能等については、中学校や高等学校の各教科等で学習しますので、小学校段階では、こうしたことへの「気付き」が重要“
「小学校プログラミング教育の手引(第三版)」
https://www.mext.go.jp/a_menu/shotou/zyouhou/detail/1403162.htm
ウィンドウズなどのオペレーティングシステム、C言語、汎用プログラミング言語とソフトウェアプラットフォームの双方を指すJava(ジャヴァ)等を生み出したのは米国です。いわゆる、ブラックボックスです。
プログラムを生み出す側と使う側みたいな感じを受けました。具体的にはこういうことなのかと思ったのが孫会長の話でした。
ソフトバンクグループ孫正義会長兼社長が、今年3月29日、テレビ東京「ワールドビジネスサテライト」で語っていました。
“視聴者からの質問にも答え、「日本から金の卵は生まれにくいのか」との問いに、「現在世界に300億円以上の価値がある未上場のAI関連企業が670社あるが、半分がアメリカ、半分の半分が中国。日本はなんと3社なんです」と指摘。「ハイテクジャパンと言われてたのが、完全に後ろのほうをついて行っている。なんとしても日本の政府、経済界、危機感を持っていますぐ取り組まなきゃいけない」と訴えた。「挽回するんだ!とまず決めることです。いま、全然、危機感ないんですよ」と。(msn.com)
(本記事は残念ながらなくなっています。デジタル社会という割には、日本メディアの記事が早々となくなるのが残念です―筆者)
<編集部補足> デイリースポーツ・WBS [テレ東BIZ](有料)
孫会長の指摘は、日本の子たちにとって重要な問題です。現在、中国が必死に米国に追いつき追い越そうとしています。競争はますます激しくなります。米国が求める優秀なプログラマーは人材不足です。したがって、所得格差がどんどん拡大しています。
10年後のお子さんがどの道に進むにせよ、小学低学年でチャンスを閉ざすようなことになってはならないと思います。
米国の先端プログラマーが、2進数の必要性をこのように云っています。
1)コンピュータが考える基本を知ること。
2)通常は、16進数、8進数を使うことが多いが、2進数を知るのが基本。
3)プログラマーにならなくとも、10進数以外の進数を知ることで、“数”というものがよりわかるようになる。
3番目の“数を知る”というのも2進数を覚えた方がいいと願った動機です。まずは、2進数になじみのない方のために、どんなものか見ることにします。
私の名をローマ字で書くと、Hideoです。コンピュータがどのような信号処理するのか説明します。
アスキー(ASCII)という文字コード表があります。ウィキペディアにあります。
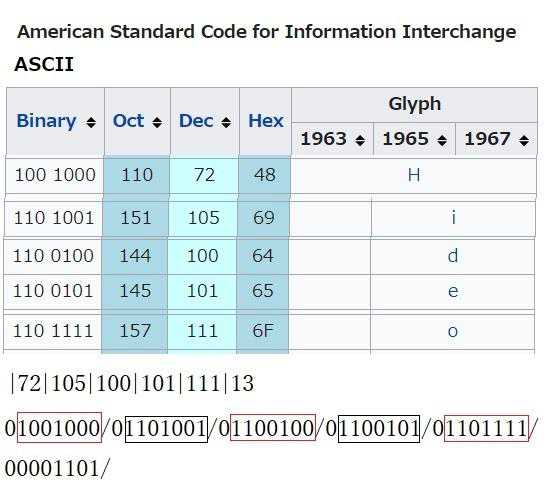
H の10進数(Dec:decimalnumber)表示が72です。これは、人が決めたファイル番号です。小文字の i が105、 d が100、 e が101、 o が111です。13は、改行コードと呼ばれるもので、Hideoはそこで終わりという意味です。
これを、2進数(Binary)で示したのが、左端の欄です。
7桁(7ビット)の1と0の組み合わせです。下の、斜線で区切ったのが、8ビットにしたものです。頭に0が入っているのはその所為です。コンピュータのオンオフ処理がこのように実行されているわけです。尚、Octは8進数(octadecimal)、Hexは16進数(hexadecimal)表示です。2進数は1で桁上がり、8進数は7で桁上がり、16進数は15で桁上がりします。10進数が9で桁上がりするのと原理は同じです。
学校で習う10進数を2進数にする変換方法よりも簡単な方法を考案しました。日本の伝統“一本締め”三次元暗唱法と名付けました。言葉と視覚による同時記憶方法です。一本締めはみなさんご存じの通りです。

このリズムで、「ゼロなしゼロじょうい~ち。いっちゼロいっちじょうに~イ」と歌う感じで暗唱します。中2の女子生徒との会話から三週間後に思いついたものです。
 10進数は0~9の10個の数字から成っているので、9で桁上がりして10になります。
一方、2進数は0と1の2個の数字しかありません。10進数の2に相当するのが桁上がりした2進数の10(イチゼロ)です。3は11(イチイチ)で、そこで桁上がりして4に相当する100(イチゼロゼロ)になります。
この記憶法の特徴は、歌い言葉の中に、“ゼロの個数”と指数(べき乗数)の一致、そして、
2進数と10進数の数の対比がある“セットの記憶法”です。
HideoのHは、10進数72ですから、64+8です。それに見合う2進数表示を持ってきて足せばいいだけです。ろくゼロ6乗64とさんゼロ3乗8を足す。それだけです。
10進数は0~9の10個の数字から成っているので、9で桁上がりして10になります。
一方、2進数は0と1の2個の数字しかありません。10進数の2に相当するのが桁上がりした2進数の10(イチゼロ)です。3は11(イチイチ)で、そこで桁上がりして4に相当する100(イチゼロゼロ)になります。
この記憶法の特徴は、歌い言葉の中に、“ゼロの個数”と指数(べき乗数)の一致、そして、
2進数と10進数の数の対比がある“セットの記憶法”です。
HideoのHは、10進数72ですから、64+8です。それに見合う2進数表示を持ってきて足せばいいだけです。ろくゼロ6乗64とさんゼロ3乗8を足す。それだけです。
 10進数は0~9の10個の数字から成っているので、9で桁上がりして10になります。
一方、2進数は0と1の2個の数字しかありません。10進数の2に相当するのが桁上がりした2進数の10(イチゼロ)です。3は11(イチイチ)で、そこで桁上がりして4に相当する100(イチゼロゼロ)になります。
この記憶法の特徴は、歌い言葉の中に、“ゼロの個数”と指数(べき乗数)の一致、そして、
2進数と10進数の数の対比がある“セットの記憶法”です。
HideoのHは、10進数72ですから、64+8です。それに見合う2進数表示を持ってきて足せばいいだけです。ろくゼロ6乗64とさんゼロ3乗8を足す。それだけです。
10進数は0~9の10個の数字から成っているので、9で桁上がりして10になります。
一方、2進数は0と1の2個の数字しかありません。10進数の2に相当するのが桁上がりした2進数の10(イチゼロ)です。3は11(イチイチ)で、そこで桁上がりして4に相当する100(イチゼロゼロ)になります。
この記憶法の特徴は、歌い言葉の中に、“ゼロの個数”と指数(べき乗数)の一致、そして、
2進数と10進数の数の対比がある“セットの記憶法”です。
HideoのHは、10進数72ですから、64+8です。それに見合う2進数表示を持ってきて足せばいいだけです。ろくゼロ6乗64とさんゼロ3乗8を足す。それだけです。
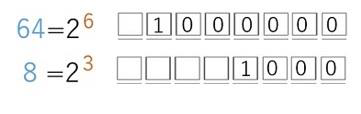
1の後のゼロの数を暗唱していますから、暗算でできます。この二つを足しますと最初に示した通り 1001000 になります。
学校で習う“10進数を2進数に変換する方法”は手間が掛かります。
2で割り続けて、余りを下から並べます。どうして下から並べるのかわからないまま、機械的にやっている人が多いのは、ITパスポートという国家試験受験用専門学校の指導法からわかりました。
実は、IT管理者教育がどのように行われているかを知ろうとして、昨年(2020年)11月に専門学校に通いました。e-ラーニングです。2進数変換をできない人も多いし、桁を間違う人も多いそうです。中2女子生徒三人に対する質問の背景には、この経緯がありました。

“一本絞め”は、ゼロの数から埋めるので桁を間違うことはありません。左が学校で習う一般的な方法です。
「整数部分を2で割る。小数点以下は2を掛ける」という学校式も論理です。それは、それで結構です。
一本締め方式も論理です。
論理さえわかれば、“一本締め”の方が簡単です。後述しますが、8進数にも16進数にもそのまま応用できます。小数点のある10進数から2進数へのの変換を見ておきます。
 整数部分は、既に説明した通りですので、ほとんど暗算でできます。
小数点以下は、2進数では半分、半分になるのでわかりやすいと思います。
当初、お母さんとお子さんが対話形式で一緒に学ぶ動画を考えたので、仮題「りょう君の楽々2進数」の対話シナリオが先にできました。しかし、質の良い動画作成にはお金が掛かるので、とりあえず、お母さん向けに簡単な紹介をしておこうと今回公開しました。
小数点以下の「りょう君の楽々2進数」の対話例を紹介します。
学校で習う小数点以下を上から並べるのもわかるかな。
整数部分は、既に説明した通りですので、ほとんど暗算でできます。
小数点以下は、2進数では半分、半分になるのでわかりやすいと思います。
当初、お母さんとお子さんが対話形式で一緒に学ぶ動画を考えたので、仮題「りょう君の楽々2進数」の対話シナリオが先にできました。しかし、質の良い動画作成にはお金が掛かるので、とりあえず、お母さん向けに簡単な紹介をしておこうと今回公開しました。
小数点以下の「りょう君の楽々2進数」の対話例を紹介します。
学校で習う小数点以下を上から並べるのもわかるかな。
 整数部分は、既に説明した通りですので、ほとんど暗算でできます。
小数点以下は、2進数では半分、半分になるのでわかりやすいと思います。
当初、お母さんとお子さんが対話形式で一緒に学ぶ動画を考えたので、仮題「りょう君の楽々2進数」の対話シナリオが先にできました。しかし、質の良い動画作成にはお金が掛かるので、とりあえず、お母さん向けに簡単な紹介をしておこうと今回公開しました。
小数点以下の「りょう君の楽々2進数」の対話例を紹介します。
学校で習う小数点以下を上から並べるのもわかるかな。
整数部分は、既に説明した通りですので、ほとんど暗算でできます。
小数点以下は、2進数では半分、半分になるのでわかりやすいと思います。
当初、お母さんとお子さんが対話形式で一緒に学ぶ動画を考えたので、仮題「りょう君の楽々2進数」の対話シナリオが先にできました。しかし、質の良い動画作成にはお金が掛かるので、とりあえず、お母さん向けに簡単な紹介をしておこうと今回公開しました。
小数点以下の「りょう君の楽々2進数」の対話例を紹介します。
学校で習う小数点以下を上から並べるのもわかるかな。
「う~ん・・・、小数点以下は位の大きい方から2を掛けたから上から並べるんじゃないのかな。」
(位ときたか)りょう君、天才だ~。じゃあ、掛ける理由をりょう君が説明して。
「説明するのは難しいよ。でも、やってみるから変だったら叔母ちゃん、助けて。」
いいよ。説明するのは難しいんだ。叔母ちゃんの苦労わかった?学校の先生は上手だね。尊敬しちゃうよね。
「じゃあ、ボク、上から並べる理由を10進数でやってみるね。
① 0.8125に10を掛けると8.125になる。だから、8は少数点以下第一位。
② 次の0.125に10を掛けた1.25の1は、小数点以下第二位の数字。
③ 0.25に10を掛けた2.5の2は第三位。
④ 0.5に10を掛けたら、5.0だから、第四位が5。だから、少数点以下が8125。この説明でいいのかな?」
完璧!原理がわかったようね。
「原理って?」
9で桁上がりするのが10進数で、1で桁上がりするのが2進数でしょう。10進数は0~9、
2進数は0~1なので、最後の数字で桁が上がるのは同じだよね。それが原理。
一本締め暗唱法と学校で習う方法も原理は一緒なの。単に、やり方が違うということなのね。
折角ですから、8 進数(Oct)と 16 進数(Hex)も2進数との対比で見ておきます。
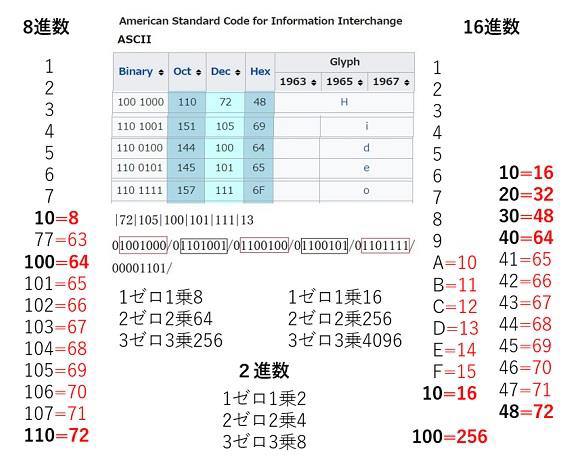
赤字で示したのが10進数です。2進数が1で桁上がりして10進数2が10(いちゼロ)、8進数は7で桁上がりして10進数8が10(いちゼロ)。16進数はF(15)で桁上がりして10進数16が10(いちゼロ)です。
対話例をもう一つ紹介します。画像が見にくいので流していただいても結構です。

「難しそう。9250なんて大きな数やってないもの。」難しくない。でも、ちょっと予習が必要ね。
10進数9250は、暗唱した10ゼロ10乗1024よりうんと大きな数字だから、9250を超すまで暗唱の延長をします。2倍、2倍するだけだから、14ゼロ14乗まで書き出す。
(左の記述と右のビット図を順に表示しながら説明する。)
①9250は13ゼロになるように1を入れる。わかりやすいように4ビットずつ合計16ビットの枠を用意しました。(ビット図①表示)
②を間違えないでね。9250から、13ゼロ8192を引く。答えが、1058。
③1058だけに注目する。10ゼロ10乗1024より大きな数字で、11ゼロ1乗2048より小さな数字だから、10ゼロになるように1を入れる。(ビット図③表示)
④1058から1024を引く。34になる。5ゼロ5乗32より大きい。
⑤6ゼロ6乗64より小さいから、5ゼロになるよう1を入れる。(ビット図⑤表示)
①34から32を引く。2。
②2がイチゼロなのはとっくに知っているよね。(ビット図⑦表示)
2進数で示す時は、最初の二つの0は不要なので、答えは、10010000100010。同じでしょう?
これを普通の割り算でやりますね。
叔母ちゃんが、手書きで計算したものを撮ったものなので、汚い字でごめんね。
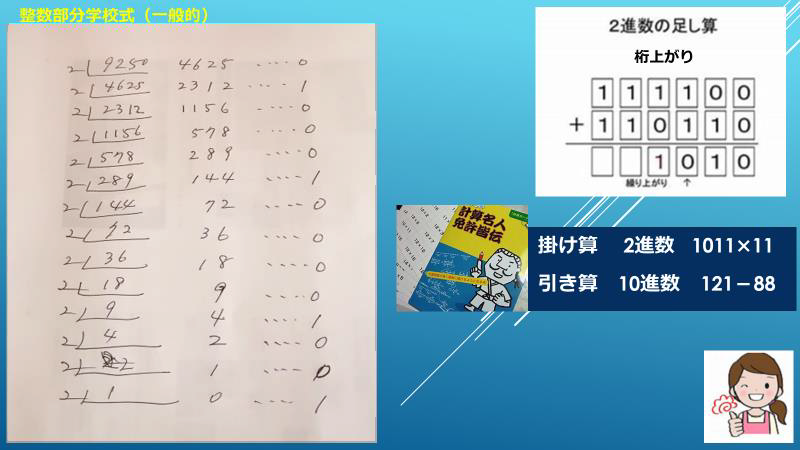
(左図)
下から並べてごらん。同じになるでしょう。14回割り算するか、一本締めでやるかは、どっちでもいいけど、両方のやり方知っていた方がいいでしょう?
ここまでで、2進数は、ほとんどマスターしたと云ってもいいのだけれど、(右上図表示)桁上がりは間違う人が多いので、その説明と、引き算と掛け算も2進数と10進数で勉強しておきましょう。
一本締めのノリの良い掛け声リズムで、10行を覚える。九々は81行です。たった10行ですから直ぐに覚えられます。元気も出ると思います。
とは云っても、こう云えるようになるには調べなければならないことがありました。
ファイナル・ファンタジーや鬼滅の刃の時代ですから、“いんいちがいち”はダサイと別の暗唱法になっているかもしれないと思ったのです、最初は。一本締めはだめかな、と。
それで、子どもたちやお母さんたちに尋ねまくりました。
小2の子のお母さんは、「今も一緒です」と答えてくれました。「ず~っと変わらないと思います」と話してくれた小6の女の子もいました。n進数という言葉を塾で教わったという利口そうな子でした。逆に、どうして調べているのですかと尋ねてきました。
「10進数を2進数にする簡単な方法を考えたのね。“いんいちがいち”みたいな感じなので受けないかなと心配したから」と答えると、本を書いてくださいと励ましてくれました。小田原での実際の会話です。
ホッとしました。一本締めで行けるかもしれない!
・・・子どもたちを中心にして2進数一本締めで日本の元気を取り戻せないだろうか。
いずれ、“博多山笠一本締め”版とか、“大阪手打ち”版など地方色豊かな動画に、地元のお母さんとお子さんに登場して貰うような「一本締め2進数全国動画大会」みたいなものをやりたいと思っています。

そういえば、今年 10 月、群馬県知事山本一太氏が、『都道府県魅力度ランキング』群馬県
44 位にブチギレ!という報道がありました。
https://www.excite.co.jp/news/article/WeeklyJitsuwa_035427/

草津小唄で、湯もみしながら、ゴ~ゼロ5乗さんじゅ~に」とおやりになったら、魅力度もアップじゃないでしょうか。教育県“ぐんま”。ソフトパワーの山本一太知事!
人気も一段と上がると思います。歌も下のURLで聴けます。
https://www.bing.com/videos/search?q=%e8%8d%89%e6%b4%a5%e5%b0%8f%e5%94%84&docid=608032472947714698&mid=2F2CE7F8C96EC47332FE2F2CE7F8C96EC47332FE&view=detail&FORM=VIRE
デジタル大臣になられた牧島かれんさんは小田原が選挙区です。小6の子との因縁もありますので、その内、お力を借りに行こうかなと思っています。袖擦れ合うも多少の縁です。
文科省は勿論、算数教育を熱心にしています。その邪魔にならず、なおかつ、お子さんの算数力をアップできるかどうかが気になりましたので、文科省の指導要領や文献を漁りまくる泥沼にはまり込みました。
この動画全国展開構想が頭に上ってから、インタビューと調査のスピードが上がりました。小学生から大学生まで150人以上に話を聞きました。小学校の先生やお母さんたちにも話を聞きました。
家にパソコンがあるか、家でパソコンを使ったことがあるか、あるならどのようにして使えるようになったか。小学生の子どもたちに尋ねました。
高校生と文科系大学生には、数学と進路決定、ややこしい図形面積の計算やった時どう思ったか、等々です。
意外に思ったのは家庭のパソコン保有率でした。30%以下という感触です。総務省の2019年調査では、モバイル端末全体が96.1%で、その内のパソコンは69.1%とあります。調査母数が15,000人強ですが、偏りがあるような気がします。
家でパソコンを使っている小4~小5生徒には、何時から使い始めたか、すぐ使えたか尋ねました時、使えないのは頭脳の問題と生意気云った男の子もいました。
「君の名前を、コンピュータがどうやって画面に表示するか知ってる?パソコンは、君を知らないけど、名前の文字を1と0で処理する。知りたい?」と話すと、目が輝きます。
“2進数”に対する子どもたちの興味はあります。確実にあります。しかし、お母さんたちがどう考えるか、正直、わかりません。
どんどん泥沼にはまり込んで、2018年のPISAの結果を知りました。
日本の子たちのレベル分布ピークはレベル3ですが、中国やシンガポールの子たちのピー
クはレベル4にあります。2020年の日本の新生児84万人に対して、中国の大学入試ガオ
カオの合格者数が800万人です。
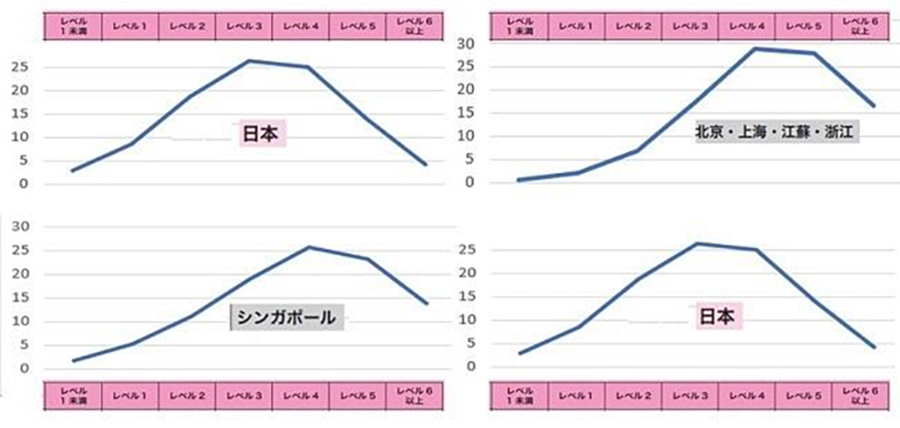 これらの調査過程で、思いもしなかった算数不安症という問題に出会ったわけです。そこから、2進数に対する取り組み姿勢が若干変わりました。
シリーズ 1(http://kamepapa.com/math/)で述べた OECD の報告書です。
これらの調査過程で、思いもしなかった算数不安症という問題に出会ったわけです。そこから、2進数に対する取り組み姿勢が若干変わりました。
シリーズ 1(http://kamepapa.com/math/)で述べた OECD の報告書です。
 これらの調査過程で、思いもしなかった算数不安症という問題に出会ったわけです。そこから、2進数に対する取り組み姿勢が若干変わりました。
シリーズ 1(http://kamepapa.com/math/)で述べた OECD の報告書です。
これらの調査過程で、思いもしなかった算数不安症という問題に出会ったわけです。そこから、2進数に対する取り組み姿勢が若干変わりました。
シリーズ 1(http://kamepapa.com/math/)で述べた OECD の報告書です。

そのため、算数不安の元凶、分数、比、割合をきちんと教える母子対話を先に公開することになりました。
英国で社会問題になっている成人の算数不安症は他人事ではない。お母さんだけに荷を背負わせるわけにもいかない。2進数を数の論理を学ぶ材料にして、レベル分布ピークを4にしたい。
少子化日本ですから、できる子だけを伸ばす英才教育は日本に合いません。どうしても、レベル3以下の子たちを押し上げてやらなければなりません。
脳科学が一般的になったので、ワーキングメモリーなどというカタカナ文字を目にすることが多くなりました。
意味は、「思考や判断など作業中(テスト中)に必要な情報を一時的に保持・処理する記憶機能のことで、短期記憶の一種」です。
算数不安に陥るとワーキングメモリーが働かなくなるというベイロック教授の研究をシリーズ1で述べました。
それを防ぐには、知識を関連付で覚えるのが必要と思います。関連付けというのは、“系統立ててセットで覚える”という意味です。
しかし、大人の世界にはなんとはない壁があります。例えば、2 進数でこれを見せると・・・
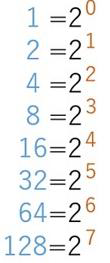
小3に指数は早すぎるという人がいます。実際いましたし、います。
私は、云い返します。
「何が早いんですか? 2×2を、”ににんがし”と習うでしょう。2×2が二乗です。同じ数を掛けた回数を云っているだけです。
セットで教えないから、子どもたちは混乱する。九々を思い出してください。掛け算を足し算ときちんと教えていないから混乱している。分数、比、割合を関連付けて教えないから5年生が割合で躓くことになる。
シリーズ1で指摘したことです。九々の問題については後述しますが、シリーズ2(http://kamepapa.com/math/vol2/)の最後に予告編として載せ
た素数の表を例にして、2という数字が如何に大切か、“セットの覚え方”が如何に大切か検討します。

素数は1と自分自身でしか割れない数ですが、1を素数とは呼びません。例えば、15は1と自分(15)の他に3と5で割れるので素数ではありませんが、2+2+2+2+2+2+2+1と表せます。それが、(2×7)+1です。どんな数字でも2と1で表すことができます。もっとも小さい素数が2です。上の表の5は、(2×2)+1。上の表にない8は、2+2+2+2であり、2を4回足すから2×4です。4は2×2ですから、2の二乗です。8は、2の二乗に2を掛けた数ですから三乗です。
同じことを云っているのです。記号が違うだけです。
+、×、指数は記号です。論理が同じなのに“セットで学ばせる”のは無理でしょうか?
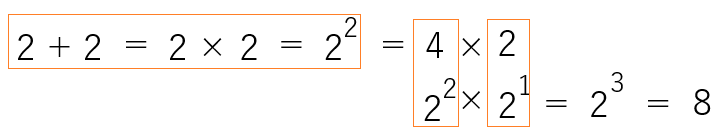
3でやります。3+3は3を2回足すから掛ける2になります。
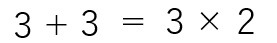
3回足すと、掛ける3になる。同じ数を掛けるから3の二乗になる。さらに、3を掛けると三乗になる。

このように教えるのが、そんなに難しいことでしょうか?
私たち大人は、こういう系統立てた学び方をしていません。教わっていません。教えてもいないし、教わってもいない。それだけのことじゃないでしょうか?
つい一週間前、日能研の電車広告に、2020年の中学入試問題がありました。半径1cmの円の図と六角形を使って円周率が3より大きいことを説明しなさいという問題です。

この問題は易しい問題じゃありません。告白しますが、私も算数不安症の一人です。電車内でこういうのを見ると、できなかったらどうしようと考えてドキドキします。
それは、それとして、なぜ難しい問題なのか説明します。
まず、円周率(π)が円の直径に対する円周の長さの比という定義を知らなければなりません。次に、半径をrとして、円周の長さが2πrになる公式を知っていなければなりません。そして、六角形の角と円の中心を結んだ六個の三角形が正三角形になるのを知らなければなりません。六角形の辺の長さ1cmは問題にあるので、合計が6cmになることはわかると思いますが、2πrのπに3を入れるというのは、なかなかできないと思います。導入して比較するというのは易しいことではありません。
πに3を入れて、半径rに1cmを入れると、2πr=6cmになります。六角形の6辺の合計の長さも6cmです。円周の方が長いので、円周率πは3より大きいという説明になるわけです。
この解答には、円周の公式があり、正三角形、正六角形があり、3を導入するという工夫が必要な上に、文章で説明しなければなりません。
この難しさに比べると、足し算が掛け算。同じ数を掛けると二乗、三乗になるというのが難しいでしょうか?
これらは、決め事です。六個の三角形が正三角形というのと次元の異なる話です。
円周の長さが2πrになるというのは、とんでもない次元の話です。
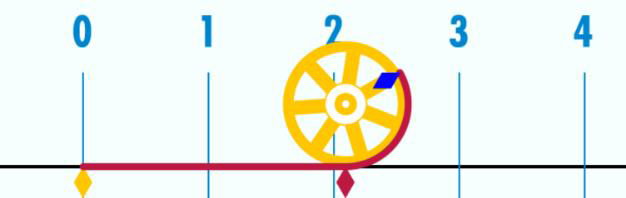
このウィキペディアのURLをクリックすると直径1の車輪が回って一周するとπ(3.14)という文字が出てきます。
1663年に日本で初めて村松茂清が『算爼(さんそ)』において「円の内接多角形の周の長さを計算する方法」で3.14…という値を算出した。『算爼』では円に内接する正8角形から角数を順次2倍していき、内接215=32768角形の周の長さで、3.141592648777698869248と小数点以下21桁まで算出している。これは現代の値と小数第7位まで同じである。
https://ja.wikipedia.org/wiki/%E5%86%86%E5%91%A8%E7%8E%87#%E5%92%8C%E 7%AE%97%E5%AE%B6%E3%81%8C%E8%A8%88%E7%AE%97%E3%81%97%E3%81%9F3.14
人間の知識欲に圧倒されます。これに比べると、2が1より一つ多い、3が2より一つ多い
というのは決めごとです。しつこいですが、数字は、符号であり記号です。同じ数を掛けると二乗、三乗になるというのも決めごとで肩につく小さな数字(指数)は同じ数字を掛けた回数を表す符号に過ぎません。
と云っても、納得しない向きもあろうかと思いますので、後述すると云った九々について述べます。
九々が日本の子たちの算数力向上の原動力になったのは事実です。西欧の数字表(numbertable)指導法と比べて九々の優位性を認める報告は多数あります。
しかし、いつのころから小学生に教えるようになったかはわかりません。
文科省の「学制百年史」によると、初等教育就学率が55%になったのが明治25年、1892年です。明治38年(1905年)に就学率96%になり、当時の識字率が男女平均90%になったそうです。高校への進学率が50%になったのが昭和33年(1958年)。90%を超えたのが昭和47年(1972年)ころです。
ウィキペディアによれば、九々の歌というのがいくつも制作されたそうです。
代表的なのが、1986年(昭和61年)にRCAビクターから(「本家!かけ算「99のう
た」」)が、アナログレコードとカセットテープで発売されたとあります。知りませんでした。
https://music.apple.com/jp/album/本家-掛け算-99のうた-幼児のときから歌でおぼえる-ep/348893601
このサイトからプレビューをクリックすると歌を聴くことができます。
私が九々を習ったのは、昭和23年(1948年)です。73年前です。暗唱です。ただ、掛け算が足し算というのを教わった記憶はありません。
今回、現役の高校生も含め、30人ほどに尋ねた質問です。
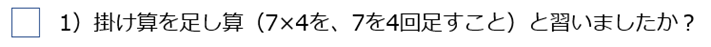
現役高校生の8割が首を傾げました。先生は教えたと思っている筈ですが、生徒に染みわたっていないのが現実と思われます。そう思う根拠はあります。根拠の一つは、パステル総研の九々の指導助言から窺えます。
「小学校2年生は算数が好きになるか嫌いになるかの最初の分かれ道。発達障害・グレーゾーンで九九がどうしても覚えられないお子さんに困っていませんか?数量のイメージが持てない子には、九九を「見える化」するのがおすすめです」というパステル総研を主宰する吉野加容子先生。
「見える化」で九九を完全マスター!という助言をしています。
「子どもが小学校に入学すると「勉強」が始まります。算数で考えてみると、小学校1、2年生の学習内容は今後の人生に影響するといってもいいぐらい大切なものになっています。小学校1年生では数の概念、繰り上がり・繰り下がりを含めた、たし算・ひき算を習います。2年生になってかけ算、わり算を学習すると、算数・数学の基礎中の基礎、「四則計算」が完成します。四則計算の学習が終了すると、今度は「四則計算」を駆使して算数の問題を解いていく段階に入ります。そのとき、繰り上がり・繰り下がりに対する苦手意識が残っていたり、九九がなかなか覚えられなかったりすると、当然問題を解くことはできません。一気に「算数」に対する苦手意識が大きくなってしまいます」というご指摘は、その通りと思います。
推奨の「見える化」というのが、おはじきみたいなものを、「2つのかたまり」が「2ずつ増えていく」ことを目で理解することができますというものなので、足し算と掛け算の本質もご助言いただきたければありがたいと思います。

根拠の二つ目が、教育・受験産業の大手の出版社であるベネッセコーポレーションが「九九の覚え方のコツは?つまずきの原因や間違えやすい段も徹底解説!」というサイトを読んだ感触です。
『数字の大きい段はすぐに対応しづらい点もつまずきやすい原因となります。たとえば「6×8」を忘れてしまった場合でも「九九のきまり」を理解していれば「6の段は、6つずつ増えていくから6×7に6を足せばいい」と考えて答えを導き出せます。しかし、6、7、8の段は数字が大きいため、足し算にも焦ってしまい間違えてしまうことが多いようです』とあります。きちんと「九九のきまり」の足し算に触れています。
いろいろなアプリなどを用いて覚え方を助言しているのですが、若干違和感を覚えたところがあります。
丸暗記だけでなく、かけ算の仕組みも理解する
九九は暗記するもの。とはいえ、ただ丸暗記をするだけでは、割り算などへのその後の応用、知識の積み重ねをしづらくなってしまいます。そうならないために、かけ算の仕組み、概念も理解しておくように声をかけていきましょう。たとえば、「3×4」なら「1つにつき3つあるものが4つ分」ということ。「1袋につきアメが3個入ったものが4袋ある。全部でいくつ?」というときの式は、3×4となります。4×3だと答えは一緒でも、意味するものが違ってしまいます。

「1つにつき3つある」というのは、シリーズ1で述べた単位概念のことです。しかし、単位概念を指導していないので、わかりにくいかもしれません。数字だけで良いようにも思います。単純に、掛け算の仕組みを、「3×4を、3を4回足す。4×3は、4を3回足す」というだけでいいじゃないのかなという違和感です。
「答えは一緒でも意味するものが違う」というのは米国のサイトにもありました。このような図を示していました。

意味が違うというほど大げさなものでもないと思いますが、順序が違うとテストでは正解にならないというのを読んだ記憶があります。そのためにも、「3を4回足す。4を3回足す」という指導をしっかりとお願いしたいものです。
単位概念は算数不安症解消のカギになる大事なものですので、読み直していただくために、ここまで公開したシリーズ1と2へのリンクをしやすくしておきます。

そして、割り算は引き算です。9÷3は、9-3-3-3=0です。ですから、3で割り
切れる。つまり、3が立って余り0です。17÷3は、17-(3×5)+2です。ですから、5が立って余り2となるわけです。
九々を学んでから100年と考えましょうか。こんな疑問すら湧きます。
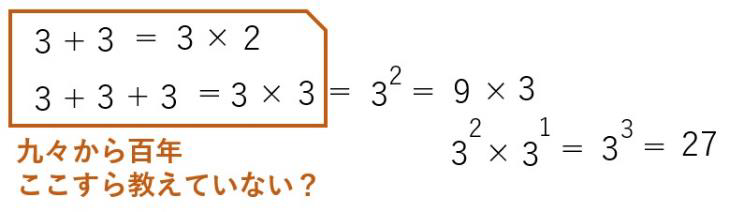
気づかなかった私も偉そうには云えませんが、100年です、100年。殻を破っても良いころではないでしょうか?
殻を破らなければ、ますます算数不安症は大きくなると懸念します。
論理が同じものを“セットで学ばせる”のは、知識拡大の常識と思いますが、素人が云っても相手にされないので、偉い先生のお言葉でもないかいろいろ探しました。
2016年5月19日に発表された日本学術会議数学教育分科会が「初等中等教育における算数・数学教育の改善についての提言」の中に、このような文言があります。
数学的な考え方の習得を教育目標として一層強調する必要がある。具体的には、第一に、「統合的・発展的な考え」である。統合的・発展的に考えることは、算数・数学のすべての内容に関わることであり、昭和43年小学校学習指導要領、昭和44中学校学習指導要領で目標に位置づけられた。算数・数学では、問題の条件を整理したり、条件を変えたり、結論から逆に考えたりして、問題解決に取り組み、解決する方法が見つかったとき、より良い方法やより一般的な方法を検討する。このような統合的・発展的な考え方の習得を、一層明確に目標に位置づけることが必要である。
http://www.scj.go.jp/ja/info/kohyo/pdf/kohyo-23-t228-4.pdf
統合的・発展的というのが、私の云う“セットで教える”のと同じかなと思いましたが、どうも意味が違うようなので、学術会議の提言がどのように使われているのか、さらに探し回りました。
幸い、神奈川県横須賀市立野比小学校の櫻井研介先生の「指導の系統性」に関する研究報告に出会いました。学術会議提言の文脈から推測すると、系統性というのはこういうことかもしれません。
私の提唱する“セットの覚え方”とは異なるものですが、このような研究を読むと、先生たちは本当に頑張っておられると頭が下がります。先生方にこうしてくださいと云う立場には
ありませんが、たまたま、母子対話に使える可能性のある問題がありましたのでお借りしました。割り算が苦手な子に対する指導です。
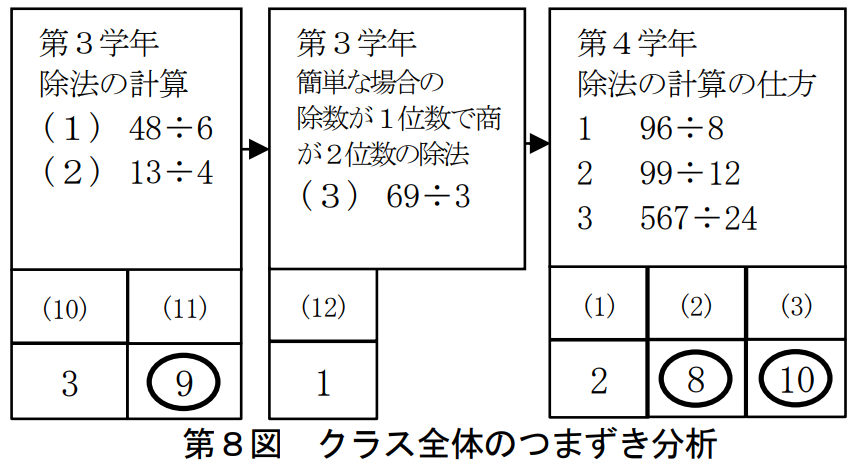
先生の研究は、「系統性や連続性がはっきりしているという特性を持つ算数・数学科においては、既習事項のつまずきが、次の学習の更なるつまずきにつながることが多く、小学校算数科でのつまずきが、中学校における数学の学習に影響を及ぼすことが懸念される。算数・数学科において、児童・生徒の既習内容の定着状況を調査し、どこからつまずいているかを分析することで、実態に応じた指導を行うことができ、その指導を継続することによって、9年間における学びの系統性・連続性を踏まえた学習指導につなげることができるだろう」というのを目的で行われたものです。論文はここから読めます。
https://edu-ctr.pen-kanagawa.ed.jp/kankoubutu/h29/chouken16/chouken16pdf/chouken16_09.pdf
先生は、研究の結果を以下のように結論しておられます。
この分析を基に、第4学年の学習内容である「567÷24」等の誤答数を減らすには、第3学年で学習する内容のうち、特に商と余りを求める除法について復習させる必要があると判断した。その結果、つまずきを解消するための指導を効果的に進めることができた。レディネステストで扱った計算問題における、クラス全体の誤答数を系統図に表示することで、担任は、それらの誤答数を比較することが可能となり、特に補充指導の必要がある内容を視覚的に捉えることができた。このことから、誤答数が系統図に示される仕組みは、教師がクラス全体のつまずきの傾向を分析する上で有効であったと考える。(茶文字は報告書の引用)
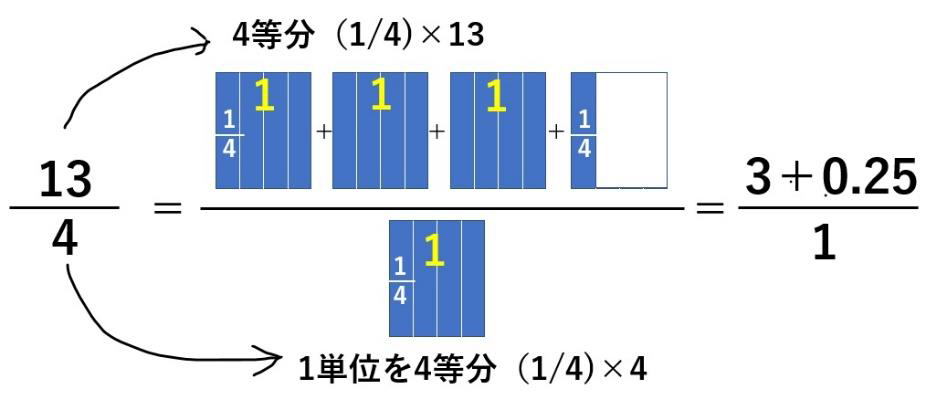
母子対話で割り算を教える場合、図を描いてやり方をきちんと教えた方が良いように思います。3年生の13÷4を例にします。
ウィキペディアからお借りした(水泳道具を運ぶ)巾着バッグを使います。この中に4個の浮袋しか入らないと仮定して、こんな対話はいかがでしょう。
「運ばなければならない浮袋が13個ありますが、巾着袋は3個しかありません。巾着バッグで運べない浮袋はいくつですか。これが、割り算13÷4の意味です」と。

「4個の浮袋しか入らない」というのは、九々でベネッセさんがおっしゃる「1つにつき3つある」と同じ単位概念のことです。云いたいことは、割る数を、一つの塊(グループ)と教えるということです。13÷4の4は、4個でも4人でもなんでもいいですが、4という一塊(かたまり)が13の中にいくつあるかというのをしっかりと教える。苦手な子は塊という考え方を理解していないかもしれません。
この理解ができれば、13÷4は、九々の4の段の掛け算問題になります。
13に近い数を探す。4×3=12
つまり3が立つ。そうすると13-12=1が余りになります。
ただし、少数にするときに余りの1を4で割るという考えを子どもたちに説明するのは難
しいように思いますが、それがわかれば0.25ですから、3+0.25=3.25が13÷4の答えになります。
このように考えると、いっそのこと分数で教える方が、はるかにわかりやすいのではないかという気がします。
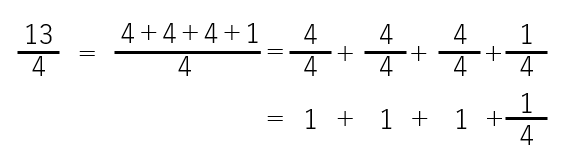
どうして、分数の話になるか説明します。シリーズ1の合理性とは別の話です。
ISO80000-2というのがあります。2009年に、それまでの数学記号についての規格であったISO31-11を置き替えるもので、割り算に÷を使わないで分数で表せとあります。
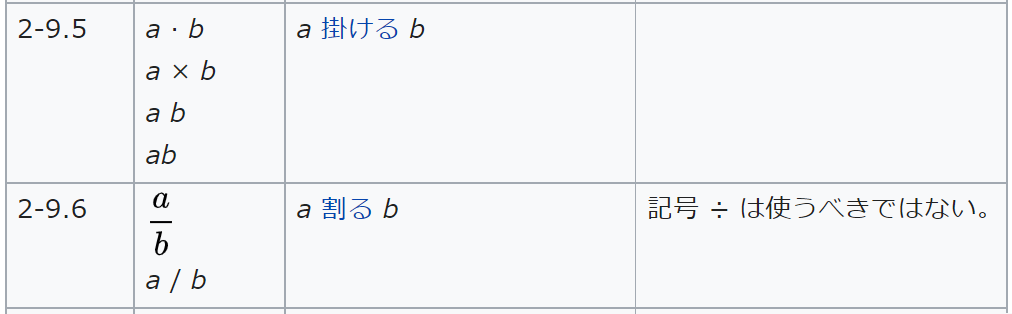
塊の話は、シリーズ1で述べた単位概念のことです。(http://kamepapa.com/math/)
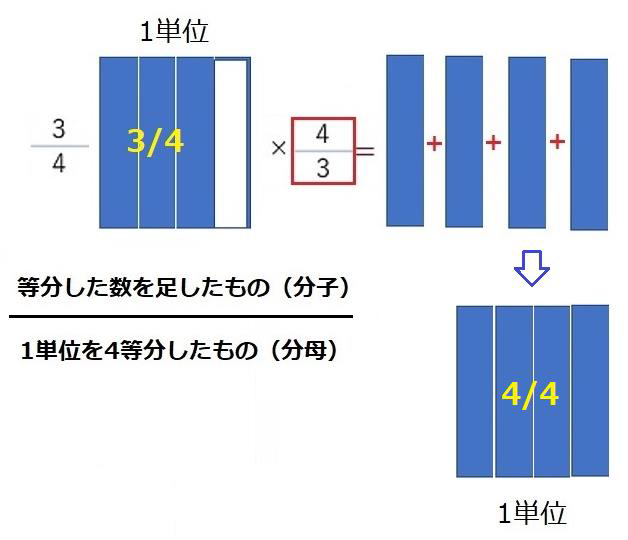
分母と分子の意味をできるだけ早い機会にきちんと説明してあげる必要があります。
13÷4を分数で表すと13/4です。分子が分母より大きい仮分数です。
仮分数であろうが、分母は、1単位を4等分したものです。分子は、等分したものを足した数です。つまり、こういうことです。
櫻井研介先生の論文は、算数不安解消のための現場の声を具体的にお聞かせいただいたものなので、大変ありがたいです。お陰様で、ここが問題というのがわかりましたので、例を挙げて、母子対話にお使いいただけるようにしました。
算数を言葉で書いたものを読むのが辛いというのはわかります。書く方も非常に辛いです。ときどき、息抜きしたくなります。

数年前に購入した油です。画家の名は忘れました。風景は日本ではありません。

下は、シリーズ1で紹介した平澤薫氏の評判の水彩作品です。遠くの山は日本アルプスだそうです。
ほっとしていただいたので、いきなり参ります。
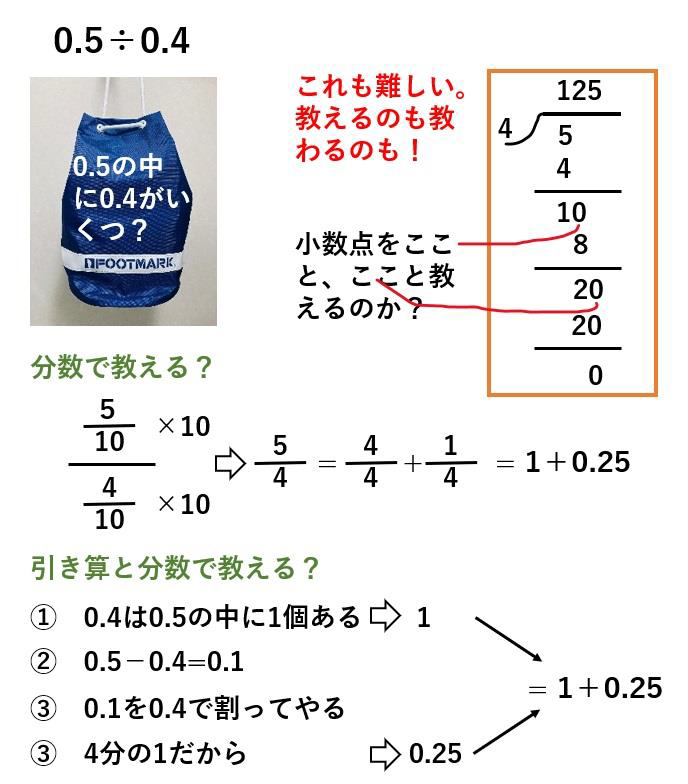
「冗談じゃない、これは教えるのが難しい」と思ったのが小数点の掛け算と割算。
12×4.3と7.2×2.4。
大人の見方で、易しいとおっしゃらないでください。自分を20年前、或いは、40年前に巻き戻してください。小学3年のあなたです。
片方が整数だとまだ楽のようですが、それでも子供たちが迷う理由がわかる気がします。
自分が先生なら、どう教えるかなと心に浮かんだものを列挙したのが左です。いずれにしても簡単なことではありません。

右の分数はわかりよいですが、そのためには、シリーズ1で散々検討した“分数、比、割合をセットで教える”必要があります。
指導要領がありますので、教室で直ぐにそうはなりませんので、今のところは母子対話で補足する以外にありません。
小数点同士になると算数不安の私は真っ青です。この指導は極端に難しいと思います。
7.2×2.4
小数点の置き方をどのように指導しますか?

この割算も教えるのは楽ではありません。
さらに、5年生で躓くので、3年生まで遡らなければならないという桁の大きな割算。
20年前に学んだとき、割算がこんなに難しいものと思いましたか?
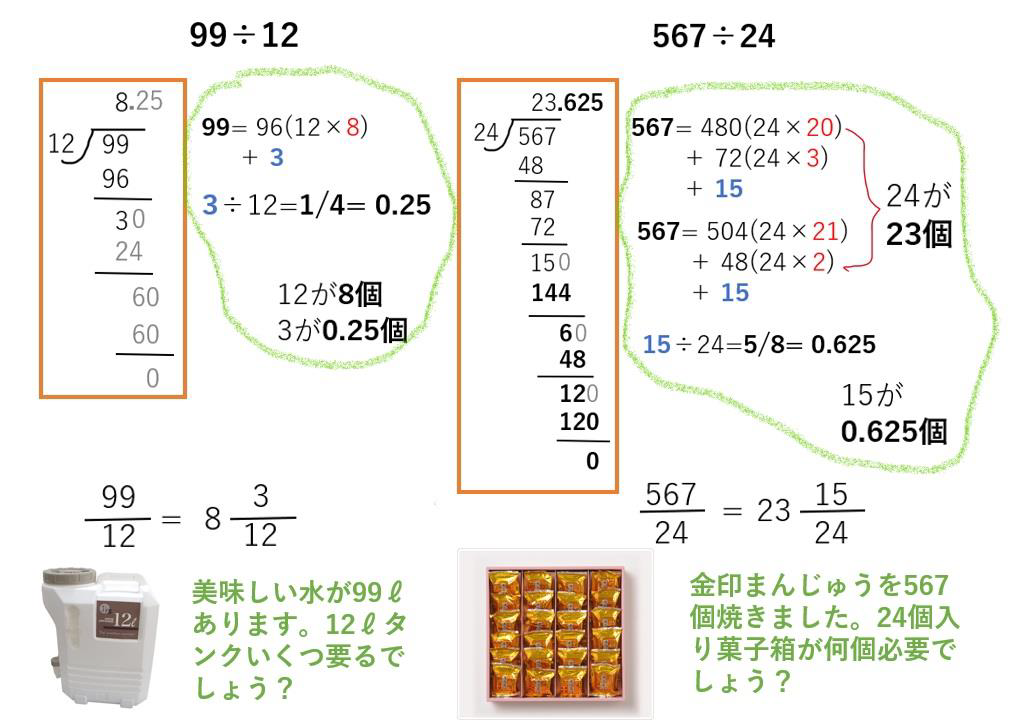
従来のやり方は実に難しいです。多分、今から40年前も80年前も桁の大きな割算が苦手な子はいたと思います。
京大と慶大が共同で行った1996年の調査がありました。文科系大学生が小学生の算数をどの程度解けるかを日本の大学生と中国の大学生を比較した調査でした。
中国の大学生の満点獲得者率が97%。それに対して日本のトップ国立大学2校の学生が、48%と28%。私大トップ2校の学生は10%以下で、最低が4.5%という結果でした。1996年は今から25年前です。
このシリーズを書くために、大学受験希望者と文科系大学生に進路決定と数学入試問題の関係を尋ねました。10人程度の少数のランダムインタビューに過ぎませんが、数学回避の傾向は明らかです。
現実の理系と文系の大学生比は1対6です。もちろん文系学生の中にも数学が得意な人はいます。しかし、全体的な傾向としては数学回避の学生が多いのは事実として捉えて間違いないと思います。
また、20人以上のお母さんたちに尋ねましたが、算数が好きで成績も良かったとおっしゃったのは二人でした。その内、一人は60歳を超えた方です。
「私も算数不安」とおっしゃった方が9人いました。
このような結果からみると、「算数不安」は、子どもたちだけの問題ではない。大人の問題であり社会の問題と思わざるを得ません。シリーズ1の引用資料に載せた英国のオックスフォード大学やケンブリッチ大学が成人の算数不安症を取り上げるのは当然と思います。
今回の調査から、男性は女性より見栄っ張りなのかもしれないと思ったのは、単なる私個人の感覚に過ぎませんが・・・
相当数の男性との会話で、はっきりと「自分も算数不安」と答えたのは、たった一人。特に、理系出身の男性は、自分が苦手だったとは認めたくないという感じを受けました。
私も理系の端くれですが、高等数学などわかりません。そして、電車内の中学入試問題を見て、「解けなかったらどうしよう」と緊張します。算数不安そのものです。不安だから、子どもの立場に自分を置くことができるのかもしれません。
指導要領をみて欲しいと思います。

本シリーズは、数と計算に焦点を絞っています。
要領の説明表現は難しいですが、あくまでも四則計算です。
自分が子どものとき、算数が苦手だったかもしれない。文系進学はその所為だったかもしれない。算数不安だったかもしれない。しかし、時が経って四則計算はできる。四則計算を容易にする工夫もできるようになった。そうなら、その工夫を子どもたちに伝えればいい。
自分が陥った不安を30年後、50年後の子どもたちに繰り返させない。これが、本シリーズの提案です。
自分は、算数ができたから不安にならなかったという理系出身の人は、「不安になる子もいる」という現実を直視してください。そして、知恵をください。これが、本シリーズの呼びかけです。
具体例を挙げているのは、知恵を出していただきたいからです。もっと良い方法があれば教えてください。いくらでも採り上げます。
さらに具体例を挙げます。
分数の掛け算と割算も鬼門です。シリーズ2の19ページに÷7があります。7で割る意味を理解しているだろうか、とだけに留めました。その続きです。
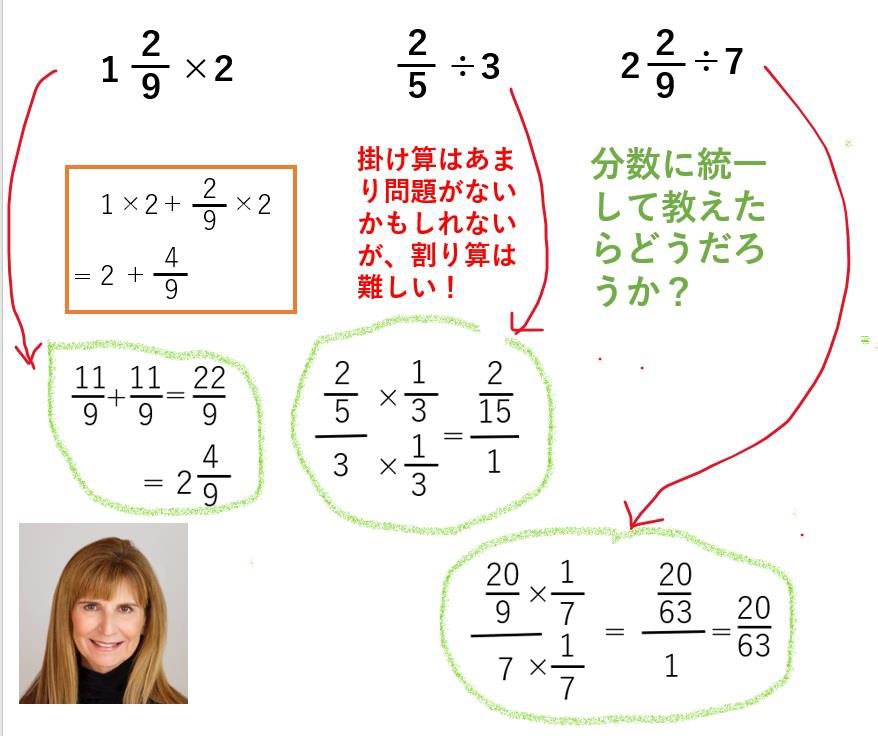
ジョーダン博士の写真を載せた理由は、「2013年まで、分数と整数を別個のものとしていた。現在は統合的にとらえる」に賛同して、“枠を超える”一つにしたい願望からです。
割られる分数が、9等分した1単位が2個と1単位の9分の2という意味であるのを図で確認します。
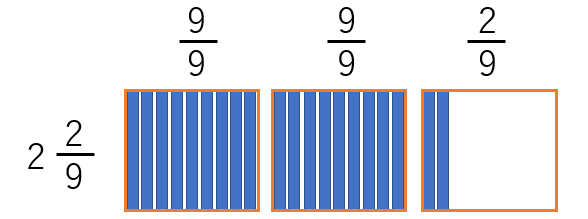
割られる分数がこういう2単位が埋まって、1単位が2しか埋まっていない状態です。ということは、
279÷7の意味は、229の中に、7(単位)がいくつあるかという問いと教えたら良いと思います。7単位というのを理解させるのは大変かもしれませんが、9分の9が1だから1単位と教えることになる。それがわかれば、2単位と9分の2しかありませんから、7単位はありません。そうすると、割合の話になって、229と7の比の問題になります。そうすると、7を分母にする分数に展開できます。上の図の単位ごとを7で割って足す。
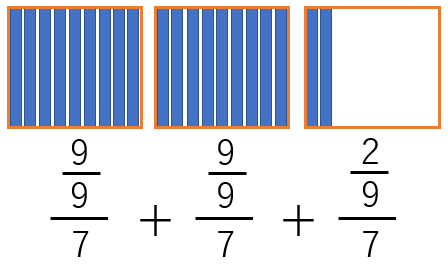
分母の7を消してやるので、前ページに示した如く、20/63になるわけです。
7は素数ですから、分子が7、14、21という7の倍数でなければ割り切れません。この問題が、答えを分数の形で求めているのか、20/63=0.317460317・・・と小数点以下を求めているかはわかりません。しかし、こういう説明で、7が素数、倍数ということもセットで覚えさせることができます。
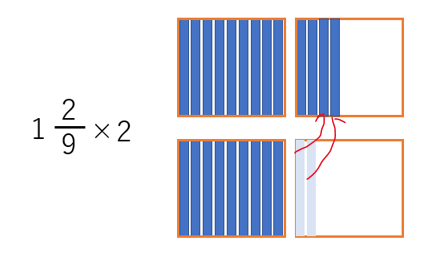
この掛け算の方は、2 個足すことですから、足せばいいだけです。2 単位と 2/9 の分子を移動してやれば、4/9 になるので、2 個と 4/9。
1かの1に2を掛けて、分子にも2を掛けると授業で教わるので、この図を見せて対話をすればきちんと理解できるだろうという提案です。
今の算数教育カリキュラムは時代にそぐわないという批判は、欧米にも日本にもあります。ただ、批判の方向がかなり異なるようです。
日本学術会議や文教大学の白石和夫教授などのカリキュラム改訂提言は、より難しい高等数学への道のりとして不十分というお考えかもしれません。
一方、欧米の批判は、今の計算力主体の算数教育は、論理思考を妨げ創造的な個性を失わせるという違いがあるように思います。
白石教授が、2003年の学会誌に厳しいことを書いています。
「現在の中学校数学の弱点は、指数・対数への流れが希薄なことである。a×10のn乗の形の表記を利用し始めると10の指数の部分が数値の大きさを定める重要な要素であることに気づく。指数として小数、分数を考えることで10のn乗の形に表してSで数値の大きさを表現するアイディアが生まれてくるであろう。この考え方は、現実に多方面で利用されている」と指摘しています。
流れの悪さというのは、私には“セットで教えない”と同義に響きます。しかし、指導の工夫次第で、かなりのことはこなせるという感触を持ちます。
を知るためというのが基本の目的ですが、2進数のn乗(指数)を見せたいと思いました。指数は習っていませんから、興味を呼び起こす意味もあると思いました。

代数になるとnが頻繁に出てきます。nというのも慣れないと不安になります。慣れても不安になるのが私です。いかにも数学という感じでいや~な気分になります。
早くに慣れた方がいいのでしょう、私も。
2進数を教えたら、指数の概念も(なんとなく)つかめるようになります。対数は、指数の反対ですから、高校で習う指数や対数の理解も容易になるかもしれません。白石教授のお悩み、一つ解決です。
但し、「指数って、なに?」と聞かれたら、こう答えてください。「何かを指すという言葉だけど、大人でもよくわからない人が多い。外国からきた用語を、誰かが指数と訳したので、それに従っただけ。算数用語は難しいので、そういうものかと覚えるよりしかたないみたい」と。私は、高1で因数分解の因数の意味が解らなくて、一学期、棒に振りました。因数が頭の中をぐるぐる回るので、分解どころじゃありませんでした。頭が分解しました。私と同じような子もいると思います。
先生に尋ねればいいじゃないかと思うでしょうが、そうはいきません。周りの子はみんな知っているのかと思うからできません。自意識過剰は私だけではないと思います。
用語理解が難しいにも関わらず、算数ができないのは読解力の問題と云い放つ元教師の方もいます。それでは、算数嫌いを増やすだけになります。他にもあります。エクスポネンシャルというやつ。理系人間が好きな言葉の一つ。英語はexponentialです。指数関数のことです。単に、指数関数的に増加すると云えばいいものを・・・というのは、算数不安症患者のひがみ根性です。
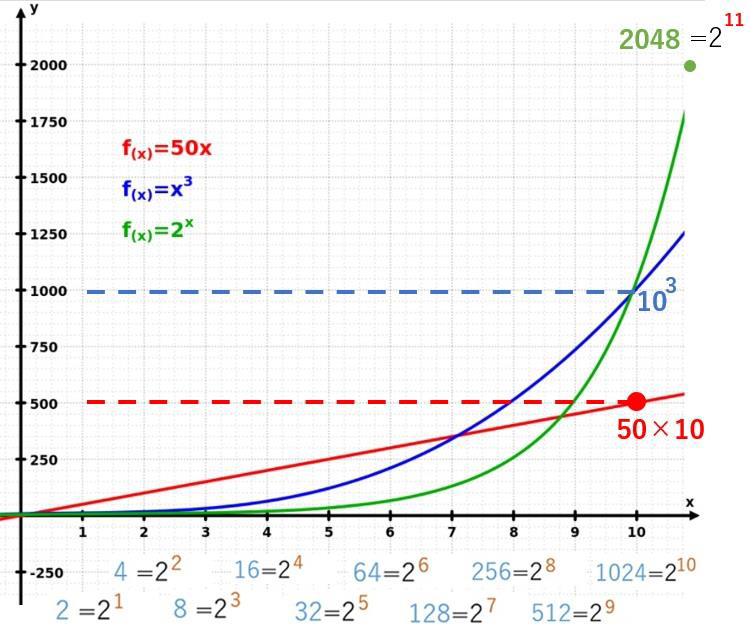
緑色が2の指数関数カーブです。青色は3乗のグラフ。10の3乗は1000です。小さな数字から大きな数字まで数を分解するときに2が使いやすいという理由がわかると思います。
指導方法の殻を破る、とは云っても長年培ってきたシステムはなかなか変わりません。デジタル時代の社会は大きく変わりました。教育システムも大きく変化していますが、母子対話がますます重要になります。
学校で教わらない2進数を教えたら、逆に子どもが混乱すると心配の向きもあろうかと思います。
しかし、シリーズ2で紹介したジョー・ボーラー教授の言葉を思い出してください。

算数というのが、いろいろ探求できるアイディアの組み合わせなのだというのを生徒がわかれば、算数不安はなくなり成績も良くなるという言葉です。
という数字が、如何に探求できるアイディアの源泉になるか。ここまで述べてきたのは、それをご理解いただくためでした。もうひとつ、お伝えしたいことがあります。
行動によって生じる結果の予測、より良い行動の選択、物事の類似点や相違点を認識する能力は、脳の前頭葉にあると云います。これは、ウィキペディアの受け売りです。
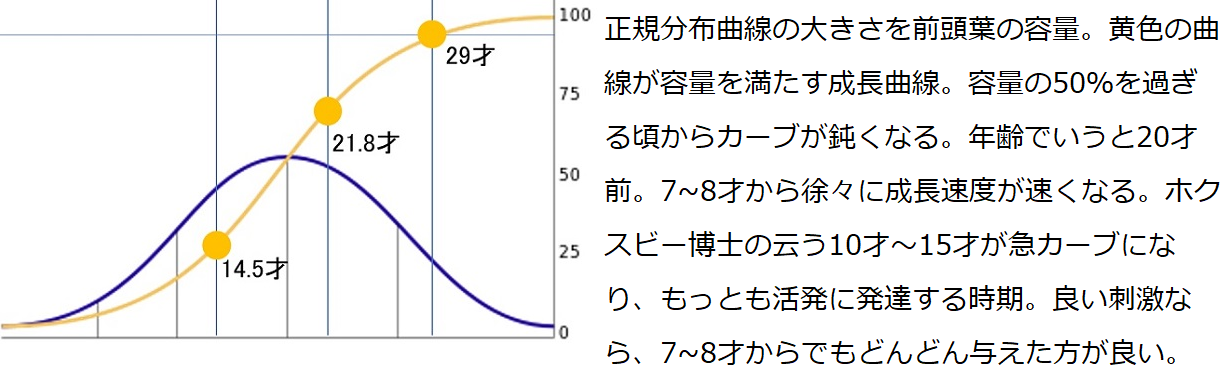
しかし、前頭葉の発達は20代後半まで続きますが、「女の子なら10歳から14歳、男の子なら11歳から15歳が“チャンス”」と云っているのは、私ではありません。
教育と政府の政策を研究分野とする米国の経済学者キャロライン・ホクスビー博士が、今年月24日、著名雑誌に寄稿していました。

こういうことです。
 ホクスビー博士の寄稿文はここで読めます。
Advanced cognitive skill deserts in the US: Their likely causes and implications Caroline Hoxby, March 24, 2021
https://www.brookings.edu/bpea-articles/advanced-cognitive-skill-deserts-in-the-us-their-likely-causes-and-implications/
シリーズ2の19ページに心理学者ジャン・ピアジェ博士の段階的認知力獲得過程研究に触れました。7~11歳児になると、「与えられる知識を鵜呑みするのでなく、自らの考えも加味して判断するようになる」といいます。これは、ホクスビー博士の前頭葉の発達経過と一致していると思われます。分数と九々を習うのが小学2年生、8歳です。4年生は10歳です。押しつけは絶対にしてはならないと思いますが、選択肢を増やして子供たちに自由な判断を委ねるのは必要ではないでしょうか。
これまで数々の素晴らしい算数本が出版されてきました。
ホクスビー博士の寄稿文はここで読めます。
Advanced cognitive skill deserts in the US: Their likely causes and implications Caroline Hoxby, March 24, 2021
https://www.brookings.edu/bpea-articles/advanced-cognitive-skill-deserts-in-the-us-their-likely-causes-and-implications/
シリーズ2の19ページに心理学者ジャン・ピアジェ博士の段階的認知力獲得過程研究に触れました。7~11歳児になると、「与えられる知識を鵜呑みするのでなく、自らの考えも加味して判断するようになる」といいます。これは、ホクスビー博士の前頭葉の発達経過と一致していると思われます。分数と九々を習うのが小学2年生、8歳です。4年生は10歳です。押しつけは絶対にしてはならないと思いますが、選択肢を増やして子供たちに自由な判断を委ねるのは必要ではないでしょうか。
これまで数々の素晴らしい算数本が出版されてきました。
 ホクスビー博士の寄稿文はここで読めます。
Advanced cognitive skill deserts in the US: Their likely causes and implications Caroline Hoxby, March 24, 2021
https://www.brookings.edu/bpea-articles/advanced-cognitive-skill-deserts-in-the-us-their-likely-causes-and-implications/
シリーズ2の19ページに心理学者ジャン・ピアジェ博士の段階的認知力獲得過程研究に触れました。7~11歳児になると、「与えられる知識を鵜呑みするのでなく、自らの考えも加味して判断するようになる」といいます。これは、ホクスビー博士の前頭葉の発達経過と一致していると思われます。分数と九々を習うのが小学2年生、8歳です。4年生は10歳です。押しつけは絶対にしてはならないと思いますが、選択肢を増やして子供たちに自由な判断を委ねるのは必要ではないでしょうか。
これまで数々の素晴らしい算数本が出版されてきました。
ホクスビー博士の寄稿文はここで読めます。
Advanced cognitive skill deserts in the US: Their likely causes and implications Caroline Hoxby, March 24, 2021
https://www.brookings.edu/bpea-articles/advanced-cognitive-skill-deserts-in-the-us-their-likely-causes-and-implications/
シリーズ2の19ページに心理学者ジャン・ピアジェ博士の段階的認知力獲得過程研究に触れました。7~11歳児になると、「与えられる知識を鵜呑みするのでなく、自らの考えも加味して判断するようになる」といいます。これは、ホクスビー博士の前頭葉の発達経過と一致していると思われます。分数と九々を習うのが小学2年生、8歳です。4年生は10歳です。押しつけは絶対にしてはならないと思いますが、選択肢を増やして子供たちに自由な判断を委ねるのは必要ではないでしょうか。
これまで数々の素晴らしい算数本が出版されてきました。
初版は1970年代と思われますが、今も購入者が多い故遠山啓博士の「算数の探検」はその最たるものと思います。それに対し、本「母子対話」シリーズは、一貫して算数不安をどのように解消したら良いのか、学力テストなどの実態を基にした具体策を親ごさんに提示するものです。遠山博士の時代にも算数不安症の子どもたちはいたはずです。京大と慶大の共同調査結果は、その表れと考えるが妥当です。加えて、算数不安症に対する脳科学アプローチはごく最近のことです。算数不安症解消は大変難しい問題ですが、優れた数学者たちには是非、その解決に立ち上がっていただきたいと願って、本シリーズを始めました。
お子さんやお孫さんのために「算数の探検」を買い求めるご両親や祖父母の方々も同じです。この意識があれば、「算数の探検」を使う場合でも、教え方に工夫が加わると思います。
若しかすると不安の原因はもっと根が深いかもしれません。一つは、ケンブリッジ大学の調査研究にある助言です。
UnderstandingMathematicsAnxiety(cam.ac.uk)
Teachers and parents need to be conscious of the fact that their own mathematics anxiety might influence student mathematics anxiety and that gendered stereotypes about mathematics suitability and ability might drive to some degree the gender gap in maths performance.
先生や両親は、自分の算数不安が子どもたちの算数不安に影響しているかもしれないことに気が付かなければなりません。さらに、女の子は算数に適していないという型に嵌った先入観が、ある程度男女生徒間の成績に影響している可能性も考慮する必要があります。
Hence, for parents and teachers, tackling their own anxieties and belief systems in mathematics might be the first step to helping their children or students.
したがって、両親も先生も自分自身の不安を何とかしなければならないこと、そして、女の子に対する先入観を捨て去ることが、子どもたちを助ける第一ステップかもしれないのです。
「自分の算数不安を告白しない男性が多い」と若干、皮肉を込めて書きましたが、本音です。長い間仕事をしてきて、1,000人や2,000人の人と付き合いはありました。ほとんど高学歴の人たちですが、数学ができる人は極めて稀です。
忘れるのでしょう。自分も算数が苦手だったことを。忘れたなら、子どもたちの算数不安など理解できないと思います。理解できなければ、指導も何もできません。精々、出版物を買い与えるだけになる。本シリーズが契機になって、真剣に分数問題を勉強し直している仲間がいます。勇気づけられます。
子どもたちは、大人より劣る存在じゃありません。大人と共に歩む存在です。歩みを止めたら、子どもたちに置いてきぼりされます。
算数不安という問題は、そういう問題と思います。偉そうに云うつもりはありません。私自身も一年前までは、見もしませんでしたから。

不安になる種子はもっとあるかもしれません。思いつく二つ目です。
考えてみれば、小学校に入学してから、いつかは“大学というところ”に行くかもしれないという漠然とした行き先みたいなものはあっても、学年が上がるたびごとに、これまで考えてもみなかった科目や授業に出くわします。常に未知の世界にいきなり連れて行かれるようなものです。
まるで、言葉もよく通じないどこかの奥地に放り出されて、さ迷い歩くみたいな感じがします。
「どこに連れて行かれるのかわからないのが不安なの?」と尋ねても、子どもたちから答えは返ってきません。わかる訳がないからです。不安の元がわかれば、不安になどなりません。大人の視点を見直す必要があると思います。
2進数で指数教えて、「高校になったら、指数と反対の対数というのをやるからね。楽しみにしてなさい」とやったら拙いですか?
教えろと云うのじゃありません。ちらっと見せるだけでいいのです。
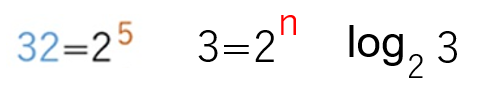
2の5乗が32は一本締めでわかりました。2のn乗が3になるnを調べる符号がlogという表示。対数は、高校で脱落する生徒が多い科目です。大人だって対数を知っているのはごく僅かです。役に立たないと云う大人もいます。日常生活でそんなに大事かなと思う面はありますが、例えば、地震の強さを表す「マグニチュード」は地震のエネルギーを1000の平方根を底とした対数で表した数値で、マグニチュードが1増えると地震のエネルギーは約31.6倍になり、マグニチュードが2増えると地震のエネルギーは1000倍になるとウィキペディアにあります。
マグニチュード - Wikipedia
「マグニチュードが 1 増えると地震の強さが 31倍にもなるのだって。良くわからないけど、対数というのを使ってエネルギーの大きさをみんながわかりやすいようにしたものらしい。高校で対数習ったら説明して?」程度の対話は良いと思いますが、いかがでしょう。
小3の子に2進数教えて、「高1になったらこんな授業するからね、今やっていたら楽勝だよ」と道標を与えてやるのは拙いですか?
どこに連れて行こうとしているのか、それとなく教えてやった方が、教わる生徒も少しは安心しませんか?
お子さんの名前を、コンピュータがどのように処理しているか教えて上げてください。
2進数は、今の時代を生きる子の常識にしないとかわいそうです。
2進数は白紙状態です。できる子は、もっと自信になります。ちょっと苦手な子には、新鮮な刺激になると思います。
シリーズ(3)完